Personal collections


Substances in all three phases (solid, liquid, gas) change their volume with temperature. The phenomenon is called thermal expansion.
We have already encountered this phenomenon in the chapter, Gas laws and ideal gas equation. We learned the relationship between the gas volume and the temperature at constant pressure. The aforementioned relationship is called the Gay-Lussac law. At constant pressure, gas expands with temperature - its volume increases. The change in volume with temperature can also be accurately calculated for an ideal gas using the gas equation:

The change in volume with temperature is therefore given as:

We divide equation 2 by 1 and get:
The factor  is called the coefficient of volume expansion of an ideal gas. For ideal gases, it is strictly determined by the reciprocal of the absolute temperature before the observed change.
is called the coefficient of volume expansion of an ideal gas. For ideal gases, it is strictly determined by the reciprocal of the absolute temperature before the observed change.
Similar to gas, the equation also applies to most liquids. Due to the temperature, the molecules collide and repel each other. The same applies to most solids. Due to the thermal fluctuation, the molecules occupy more space, and the total volume increases.
There are also exceptions when the volume of a substance decreases with temperature. We say they have a negative temperature expansion coefficient.
Let's take a rod of length 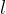 and increase its temperature by
and increase its temperature by 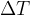 . The rod will extend by
. The rod will extend by 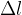 as shown in the figure below.
as shown in the figure below.
The quotient of the extension 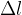 and the original length
and the original length 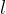 is called the relative extension. The relative extension is proportional to the change in temperature
is called the relative extension. The relative extension is proportional to the change in temperature 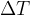 :
:
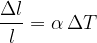
or

The factor 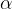 is called the linear expansion coefficient.
is called the linear expansion coefficient.
The final length 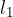 of the rod after the thermal expansion is given as:
of the rod after the thermal expansion is given as:
The relative linear extension is proportional to the change in temperature and is given as:
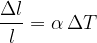
where 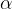 is the linear expansion coefficient. Consequently, the final length of the heated rod is given as:
is the linear expansion coefficient. Consequently, the final length of the heated rod is given as:

The table of the linear expansion coefficients for some materials is shown below.
Let's take a cuboid with dimensions of length a, b, and c. When the cuboid is heated, the dimensions are increased by 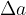 ,
, 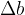 , and
, and 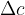 as shown in the figure below. This also increases the volume.
as shown in the figure below. This also increases the volume.
From the figure above, we can obtain an approximate expression of how much the volume has increased. The change in volume 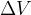 is given according to the figure above, as:
is given according to the figure above, as:
In the calculation, it can be observed that we neglected the small cuboids along the edges. The total volume of these cuboids is given according to the figure above, as:
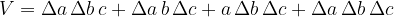
The final volume of the cuboid after thermal expansion is therefore given as:
The relative volume expansion of a body is proportional to the change in temperature and is given as:

where 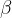 is the volume expansion coefficient and is approximately given as:
is the volume expansion coefficient and is approximately given as:
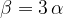
The final volume of a body after heating is given by the formula:
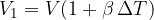
The table of volume expansion coefficients of some substances is given in the table below: