Trigonometric equations are equations in which angular functions occur, and the argument of a function (angle) is unknown. We rearrange each one to basic.
The most basic equations are found when looking for zeros, maximum and minimum values of functions. Whenever we write down the solution of an equation, we must also consider the periodicity of the basic functions.
Each basic trigonometric equation has the form:
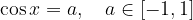
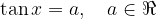
The solution of the equation can be found in several ways.
Solve the equation:
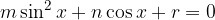
We solve according to the following procedure.
We rearrange the equation into a quadratic equation:
We get the quadratic equation and solve the quadratic equation with the form:
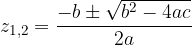
where the coefficients are
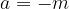
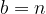
The solutions of the quadratic equation are as follows:
It remains for us to solve the basic equation.
Solve the equations
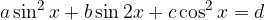
We solve according to the following procedure:
When we insert numbers, we get the solutions of the quadratic equation:
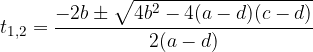
which are solutions of the original equation.
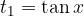
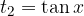
It remains for us to solve the basic equation, which leads us to the final solutions of the equation.
Solve the equations:
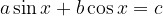
We transform the equation using angle functions of double angles into a homogeneous equation:
When we calculate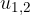 
, we still have to solve to the basic equation:
Solve the equation:
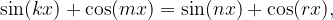
we will look at an example:
