Circular motion is an example of curvilinear motion. When circling, a body moves along the circumference of a circle, i.e. along a circular path. At a moment, the direction and speed of motion of the body are described by the velocity vector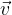 
. It is also called the circumferential or tangential speed.
The velocity vector follows a circle, so its direction is constantly changing. It is drawn as a directed line, and its direction is tangent to the circle at the point where the body is currently located (see Figure 1).
Figure 1: Circular velocity vector
Depending on the absolute value (magnitude) of the speed, circular motion can be:
uniform: the absolute value of the velocity vector 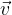is constant - it does not change with time.
non-uniform: the absolute value of the velocity vector 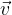changes with time: it can increase or decrease uniformly. In this case, it is uniformly accelerated circular motion.
In this chapter, we will learn about uniform circular motion.
A body moves uniformly along a circular path of radius 
, as shown in Figure 2.
Figure 2: Uniform circular motion
From Figure 2, we can see the basic geometric elements used to describe circular motion:
the velocity vector 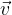or tangential velocity is the velocity with which the body rotates the circle;
the radius of the circle, which determines the path of the motion;
the distance 
that the body completes in time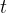 
is equal to the length of the circular arc described by a point on the circle during motion;
the angular displacement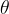 
described by the body in time .
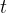In addition to the basic geometric elements, the following important physical quantities occur during circular motion:
Period
The body moves in a circle and after a certain time, it comes back to the starting point where it started moving. The time when the body completes one round of the circle is called the period and is denoted by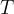 
.
The period is therefore the time in which a point or body makes a complete rotation around the circle and comes back to its starting point.
Frequency
In general, the frequency tells us how many complete rotations the body makes in an observed time. However, since we usually convert the units into basic measurement units, the frequency tells us the number of complete rotations that a rotating point (e.g. a point on a fan) makes in one second. The notation for frequency is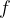 
.
Angular velocity
We have already mentioned that during the motion of the body in a circle, the angle also changes. How fast the angle is increasing or decreasing with time is what the angular velocity tells us. The concept of angular velocity is similar to the concept of speed, except that now we do not observe the distance traveled in a given time, but rather the described angle in a given time. In circular motion, we prefer the unit radians instead of degrees. So angular velocity tells us how many radians an angle makes in one second. It is denoted by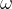 
(pronounced omega).
Centripetal or radial acceleration
From Figure 2, we notice that the velocity vector changes with time (the magnitude may remain the same, but the direction changes). We know that the change in velocity over time equals acceleration.
Velocity changes due to radial acceleration. Radial acceleration is the one that allows the point to move on a curved path - a circle. It is directed perpendicular to the tangential velocity vector and points in the direction of the radius.
If the rotating body were to suddenly lose radial acceleration, it would continue to move in a direction tangent to the circle.
The period, frequency, and angular velocity are quantities that describe similar laws and are derived from each other. If we know one of the quantities, we also know the other two. It makes sense to get to know them together.
The period is the time it takes for a point to make a complete rotation around a circle and reappear at the starting point. We denote it by .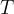
During a period, the rotating body:
makes a distance equal to the circumference of the circle along which it rotates,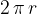 
; and
makes a complete angular displacement of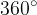 
or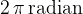 
.
The frequency 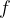is extremely closely related to the period :
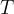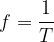
The unit of frequency is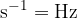 
(Hertz).
The frequency can also be calculated by counting the number 
of the complete rotation of the circle and dividing it by the observed time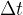 
:
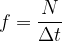
Let's observe the angle 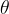described by the line between the observed point and the centre of the circle, this is called the angular displacement.
The angular displacement changes over time as the point travels around the circle: increasing or decreasing. How much the angular displacement increases or decreases in the observed time determines the angular velocity :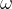
Let's write this as an equation:
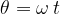
So, the angular velocity is generally given as:
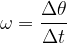
The unit of angular velocity is:
We dropped the radian because it is not a physical unit.
We always express angles in radians in circular motion!
Let's recall that an angle can be measured in degrees or in radians. If we measure an angle in degrees, the total angle of a circle is 360 degrees. If we measure in radians, the total angle is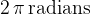 
.
The only difference between degrees and radians is that they are different units of measurement. We convert degrees to radians or vice versa linearly, using the equations:
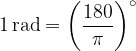
We can get more about degrees and radians in the material, measurement in geometry.
Let's express the angular velocity in terms of frequency. For this purpose, we use the formula of angular velocity which is given as:
In uniform circular motion, the angular velocity is constant.
Let's repeat the concepts and formulas for a point moving uniformly around a circle.
The period 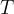is the time of one complete rotation.
The angular displacement 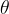is given as the product of the angular velocity 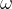and time :
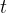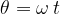
Frequency 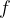and period 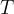are reciprocals of each other:
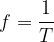
The frequency 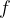is also the number of complete rotation made in the observed time: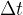
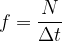
The angular velocity 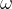, period 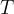, and frequency 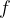are related by the formulas:
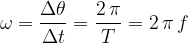
In uniform circular motion, the angular velocity is constant.
Tangential speed is the speed at which a point moves in a circle. In uniform circular motion, the motion in the circle is uniform, the speed is constant, and only the direction of the speed follows the path of the circle.
In this case, the path distance made by a point on the circumference of the circle (see Figure 1) is the same as in the case of uniform motion:
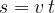
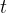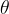This distance is also the length of the circular arc of the circle that the body completes in time . Let's recall how to calculate it: the length of an arc is the radius times the angle (in radians) it subtends:
The tangential velocity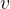 
is the product of the angular velocity 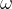and the radius of the circle:
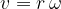
We have already mentioned several times that the speed of motion along the circle is constant in magnitude but not in direction. Let's observe how the direction of motion changes during the rotation!
Figure 3: Radial or centripetal acceleration of circular motion
On the left image in Figure 3, two velocity vectors are drawn that differ only by the angle:
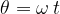
Let's move the starting points of both vectors to the same point, as shown in the right figure in Figure 3 - to make it easier to distinguish them, we'll label them with indices 1 and 2 (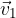
and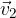 
). The angle between them again equals .
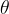The direction of the vector 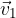changes and becomes 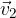because at every moment, a velocity vector directed in the direction of the radius to the center of rotation is added to it:
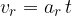
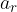is called the radial or centripetal acceleration.
Let's calculate the radial acceleration using the right figure in Figure 3. Let's use the formula for the arc length of a circle:
or we can write this mathematically as:
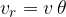
Let's obtain an expression for the centripetal acceleration:
The radial acceleration acts towards the centre of the circle and causes the velocity vector to vary in direction and tangent to the circle at all times.
Depending on the data we have, we calculate radial acceleration using any of the formulas below:
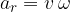
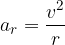
A special form of uniform circular motion is rolling.
Let's take a closer look at what happens when rolling and observe a point on the circumference of the rolling wheel (see Figure 4). We can say for sure that the point is rotating because the wheel is rotating. But if the point just rotates, it would end up in the same place again after 360° - but it doesn't. In the meantime, the wheel has moved in the direction of rolling forward. Obviously, the point not only rotates but also moves linearly. Rolling therefore consists of two motions:
circular (rotational) motion and
translational (straight line) motion.
The point moves along a curved path, its speed fluctuating between zero at the point of contact between the wheel and the ground and twice the speed at which the wheel is traveling. In each position, it is equal to the vector sum of both rotational and translational velocities (see Figure 4).
Figure 4: Composite motion - rotation and translation during rolling
During uniform rolling, a body moves:
linearly and uniformly,
and at the same time, it rotates uniformly.
To better understand this motion, let's observe the velocities of points in three different positions: in points A, B, and T in Figure 5:
Figure 5 Speed of motion of selected points during rolling
Let's describe what is happening to the points:
Point A
Point A lies at the point of contact between the wheel and the ground. Two speeds add up here:
the speed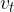 
of linear (translational) motion, and
the tangential speed 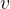of rotation.
If the wheel does not slip, the speeds are:
equal, in absolute value; and
opposite in direction: the point speed is directed to the left and the wheel is moving to the right.
Both speeds are subtracted, their sum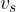 
is zero.
Point B
Point B lies at the top of the wheel. The speed 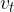of translational motion and the tangential speed 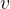of rotation are:
absolutely equal and
equally directed.
The speed 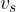at this point is therefore equal to twice the speed of motion 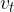or twice the tangential speed of rotation :
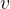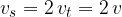
Point T
Point T is the centre of gravity of the wheel. This point only moves in a straight line - not a circle. Its speed is .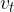
If a body does not slip when rolling, the following applies:
the tangential speed is equal to the speed of motion of the centre of gravity;
the point at the junction of the rolling body and the base is at rest;
a point at a distance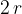 
from the ground moves at twice the speed of motion.
