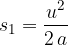Personal collections


In the chapter, Uniform motion, we studied a body moving at a constant speed along a straight line. We called this motion linear uniform motion.
But in general, the speed of motion is not constant but changes with time. In this case, the motion is non-uniform.
Figure 1 shows the speed-time graph of a body for some non-uniform motion, where the body's speed changes in sections. If its speed increases, we speak of acceleration, but if it decreases, the acceleration is negative and we call it deceleration.
The magnitude of the acceleration (or deceleration) depends on the change in speed during the observed time:

The unit of acceleration is:
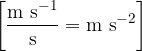
Let's go back to Figure 1. We know from mathematics that the slope of a line is calculated using the formula:
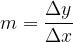
If we look at the graph above in Figure 1, we have labelled the x-axis with 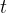 (the x-axis represents time) and the y-axis with
(the x-axis represents time) and the y-axis with 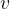 (the y-axis represents the speed). Let's write down the equation for the slope again, with the symbols from Figure 1:
(the y-axis represents the speed). Let's write down the equation for the slope again, with the symbols from Figure 1:
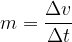
We got nothing but equation (1), which means that the acceleration on the graph at the top in Figure 1 is exactly the slope of the individual lines. This can be clearly seen in comparison with the graph below in Figure 1: the lower the slope of the line (in the graph at the top), the lower the acceleration (in the graph below in Figure 1).
In the graph below in Figure 1, we can also see that:
during the time interval 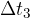 the speed does not change, so the acceleration is zero.
the speed does not change, so the acceleration is zero.
during the time interval 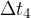 the velocity decreases, so the acceleration is negative. We call it deceleration.
the velocity decreases, so the acceleration is negative. We call it deceleration.
The acceleration of motion is the change in the speed of motion in the observed time:

The acceleration of a body is obtained by observing the slope (slope) of the graph of the function 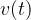 .
.
The unit of acceleration is:
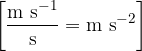
The calculations in this chapter are intended for students with advanced knowledge. The reader can skip this chapter without any effect on the understanding of the rest of the material.
In most real situations, however, the speed changes continuously (more smoothly and not in sections as in Figure 1). A somewhat more realistic graph of speed and acceleration is shown in Figure 2 below:
First, let's describe what is happening in Figure 2: the acceleration is initially positive and decreases. Therefore, the slope 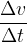 decreases from
decreases from 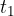 to
to 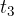 . At time
. At time 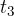 , the acceleration is zero because the slope is zero. In time
, the acceleration is zero because the slope is zero. In time 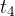 , the slope is negative - the graph of
, the slope is negative - the graph of 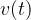 decreases with time.
decreases with time.
We calculate the acceleration of such a general curve as follows: when observing the slope of the curve, we take sufficiently small sections of the observation 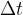 , so that we can consider that the speed within
, so that we can consider that the speed within 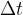 changes linearly. But this happens only when the observed interval decreases towards an infinitely small value (but never reaches the value 0). This is actually just the derivative of the function
changes linearly. But this happens only when the observed interval decreases towards an infinitely small value (but never reaches the value 0). This is actually just the derivative of the function 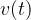 after time
after time 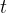 :
:
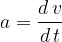
The equation is very similar to equation (1), but to emphasize that we are talking about infinitesimally small differences, we use the notation  (d difference ) instead of
(d difference ) instead of  in the equation.
in the equation.
Uniformly accelerated motion is a special case of non-uniform motion, where the acceleration 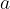 is the same (constant) all the time. In uniformly accelerated motion, velocity varies linearly with time.
is the same (constant) all the time. In uniformly accelerated motion, velocity varies linearly with time.
We start from equation (1):
The general equation for uniformly accelerated motion (that is when the acceleration 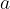 is constant) is:
is constant) is:

Let's look at some special examples of uniformly accelerated motion.
Let us consider the special case of the equation:
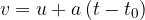
when the initial velocity 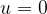 , and the time
, and the time 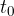 when we start measuring the motion is set to 0. The equation therefore becomes:
when we start measuring the motion is set to 0. The equation therefore becomes:
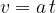
We can notice that we have obtained an example of a linear function, where the constant  is equal to 0; we start drawing the line from the origin, and the slope gives the acceleration
is equal to 0; we start drawing the line from the origin, and the slope gives the acceleration 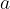 :
:
From the graph, we can read the time 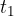 at which the body reaches its final speed
at which the body reaches its final speed 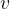 , so we can write the acceleration
, so we can write the acceleration 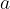 as:
as:
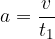
Let's calculate the distance travelled. During the time interval 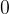 to
to 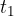 , the speed varied from
, the speed varied from 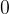 to
to 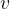 . During this time, the body travels a distance
. During this time, the body travels a distance 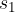 equal to the product of the average speed
equal to the product of the average speed 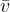 and time
and time 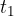 :
:
We generalize the resulting equation by expressing the distance 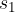 as
as  and time
and time 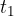 as
as 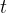 :
:

Equation (4) represents a quadratic function. In uniformly accelerated motion, the distance travelled varies with the square of time. Let's see:
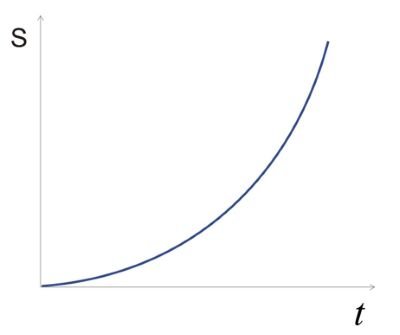
Figure 4: The distance-time graph is a parabola
From equation (3) we can obtain a formula for the time 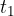 when the body completes the distance
when the body completes the distance 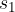 :
:
The final speed 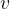 is given as:
is given as:
Let's generalize the expression. The time 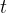 taken by the body to travel a distance
taken by the body to travel a distance  is given as:
is given as:
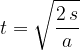
The final speed 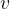 in terms of the distance
in terms of the distance  of the body is given as:
of the body is given as:
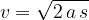
In a uniformly accelerated motion with an initial velocity of zero, it is considered that:
the speed 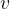 in terms of the time
in terms of the time 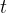 is given as:
is given as:
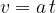
the distance  covered by the body is given as:
covered by the body is given as:
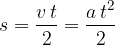
the time 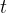 taken to cover distance
taken to cover distance  is given as:
is given as:
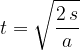
the speed 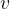 in terms of the distance
in terms of the distance  is given as:
is given as:
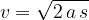
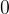
When calculating the distance travelled by a uniformly accelerated body in time 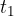 , we need the average speed
, we need the average speed 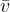 of the body in the measured time. Without going into a more detailed calculation at this point, let's just write down the average speed of the body that has the initial speed
of the body in the measured time. Without going into a more detailed calculation at this point, let's just write down the average speed of the body that has the initial speed 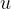 at the start of the measurement and reaches the final speed
at the start of the measurement and reaches the final speed 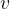 :
:
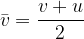
If the initial speed 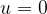 , then:
, then:
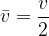
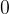 )
)The distance travelled by a uniformly accelerated body can also be calculated using a graph; let's look at Figure 3. The area under the graph 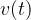 (the region is coloured green) is exactly the same as the distance travelled. This conclusion also applies in general:
(the region is coloured green) is exactly the same as the distance travelled. This conclusion also applies in general:
The distance in any (uniform or non-uniform) motion is obtained by calculating the area under the velocity-time graph.
Let's calculate the area. We can see that the green area in Figure 3 is a triangle. The area of a triangle is half base times the height. If we map this to our example, we again get:
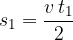
Let us consider a special case of the equation:
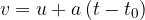
where the body has an initial speed 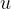 at the beginning of the measurement, and the times
at the beginning of the measurement, and the times 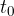 when we start measuring the motion is set to 0. The equation therefore becomes:
when we start measuring the motion is set to 0. The equation therefore becomes:
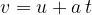
We can see that we have obtained an example of a linear function, where the constant  is equal to
is equal to 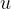 . As we know, the constant tells us where the graph intersects the y-axis. Therefore, we start drawing the graph at point
. As we know, the constant tells us where the graph intersects the y-axis. Therefore, we start drawing the graph at point 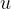 , and the slope gives the acceleration
, and the slope gives the acceleration 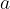 :
:
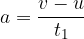
The distance travelled by the body in time 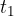 is equal to the area under the velocity-time graph (see Figure 5). It consists of the distance that the body would travel if it were moving at a constant speed
is equal to the area under the velocity-time graph (see Figure 5). It consists of the distance that the body would travel if it were moving at a constant speed 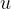 and the component of uniformly accelerated motion.
and the component of uniformly accelerated motion.
The equation can be written more generally by expressing the distance as a function of any observed time:
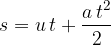
Let's also calculate the velocity 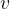 as a function of the distance
as a function of the distance  with the known acceleration
with the known acceleration 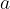 and the initial velocity
and the initial velocity 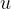 :
:
In uniformly accelerated motion with an initial velocity 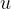 , it is noted that:
, it is noted that:
the velocity acquired by a body at time 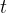 can be calculated using the following two equations:
can be calculated using the following two equations:
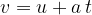
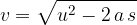
the distance travelled by the body in time 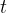 is given as:
is given as:
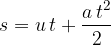
When calculating the distance that a uniformly accelerated body completes in time 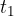 , we will need the average speed of the body in the measured time. Without going into a more detailed calculation at this point, let's just write down the average speed of a body that has an initial speed
, we will need the average speed of the body in the measured time. Without going into a more detailed calculation at this point, let's just write down the average speed of a body that has an initial speed 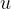 at the start of the measurement and reaches the final speed
at the start of the measurement and reaches the final speed 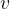 :
:
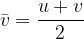
This is actually the arithmetic mean of the initial and final velocities.
As before, when we calculated the distance travelled by a uniformly accelerated body, we can now calculate the distance using a graph; let's look at Figure 5. The area under the velocity-time graph (the area is coloured green) is exactly the same as the distance travelled. The area under the graph consists of a rectangle and a triangle:
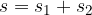
The area of both sections is easily identifiable; the area of the rectangle is:
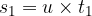
and the area of the triangle is:
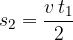
We insert both areas and get the already known formula again:
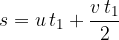
At the start of the measurement, the body has an initial velocity 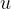 . As the body moves with constant deceleration, the body's speed decreases. We also say that the body decelerates. Let's see how the graph of velocity-time graph (
. As the body moves with constant deceleration, the body's speed decreases. We also say that the body decelerates. Let's see how the graph of velocity-time graph (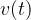 ) looks like:
) looks like:
The acceleration of such motion is negative (see Figure 6). We also call it a deceleration. Let's obtain the formula for deceleration:
Acceleration is negative. We call it deceleration.
The formulas for velocity and distance are the same as in the previous chapter. We only consider that the acceleration is negative.
The speed 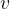 in terms of time
in terms of time 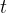 is given as:
is given as:
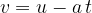
The distance  in terms of time
in terms of time 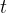 is given as:
is given as:
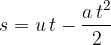
The speed 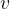 in terms of the distance
in terms of the distance  at a given acceleration
at a given acceleration 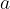 is given as:
is given as:
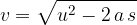
Let's obtain the time 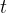 when the speed
when the speed 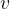 drops to zero:
drops to zero:
Therefore, the time required to stop the body is:
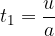
The maximum distance it travels before stopping is equal to the area under the velocity-time graph - Figure 5.
The formulas for uniformly decelerating motion with an initial velocity 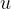 are the same as the formulas for uniformly accelerated motion, only the acceleration
are the same as the formulas for uniformly accelerated motion, only the acceleration 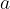 has an accompanying sign and appears in the formulas with a minus sign (
has an accompanying sign and appears in the formulas with a minus sign (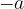 ):
):
the velocity of the body is calculated using the following two formulas:
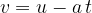
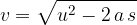
the distance that the body travels in time 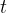 is given as:
is given as:
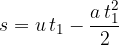
the time at which the body stops is given as:
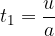
the stopping (or braking) distance is given as: