Personal collections


Bodies in nature can be at rest, moving uniformly or non-uniformly. A car in motion, for example, can accelerate, move at a constant speed or decelerate. The driver of the car adapts his driving to the road conditions. The same goes for most moving bodies.
Let’s observe the motion of a runner in a marathon. The marathoner starts running at a moderate speed. The speed is not too high as he tries to store energy for the other half of the race. His movement is fairly steady at first. He gradually accelerates only in the second half of the race, overtakes other runners who initially left him behind and then finishes the race. At this moment, he runs at his full power to achieve the best possible result.
A long-distance runner therefore moves non-uniformly. His speed changes with time. Only at some short periods of time can we assume that he is moving at least approximately uniformly.
In this chapter, we will discuss non-uniform motion. We will focus on non-uniform motion in which the speed increases or decreases steadily with time. This is called uniformly accelerated or uniformly decelerated motion.
Non-uniform Motion
A body can move at uniform speed or non-uniform speed.
During uniform motion, the speed does not change with time. The distance covered is the product of speed and time. This is written with the equation:
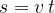
What if the speed changes over time? Such a motion is called a non-uniform motion. During non-uniform motion, the speed may increase or decrease over time. This is called accelerated motion or decelerated motion.
During non-uniform motion, the speed changes over time. If the speed increases with time, it is an accelerated motion. If the speed decreases with time, it is a decelerated motion.
A special case of non-uniform motion is uniformly accelerated motion. In this case, the speed increases steadily with time. This means that the body's speed increases by the same amount at equal time intervals.
During uniformly accelerated motion, the speed changes uniformly. The speed is different at each observed moment. This is called the instantaneous speed.
During uniformly accelerated motion, the velocity increases uniformly with time. This means that the increase in the speed is the same over time-long intervals. The graph of velocity against time is an ascending straight line.
The current value of the speed is the speed at some observed time 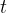 .
.
We introduce a new physical quantity called acceleration. Acceleration tells us the increase in speed within the observed time interval. The acceleration is denoted by 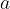 :
:

The sign 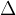 (Greek letter Delta) means the difference between the final and initial value:
(Greek letter Delta) means the difference between the final and initial value:
Change in speed
It is calculated as: "speed at the end of the observed time interval, denoted by 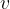 " minus "speed at the beginning of the interval, denoted by
" minus "speed at the beginning of the interval, denoted by 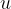 ".
".
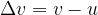
The change in speed retains the same unit as the speed: 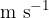
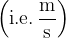 .
.
Change in time
It is calculated as: "time at the end of the observed time interval" minus "time at the beginning of the interval"
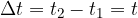
The time change retains the same unit as the time:  .
.
We write the general equation with which we calculate the acceleration at uniformly accelerated or decelerated motion and then insert the expressions for changes in speed and time:
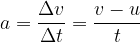
Let's derive the unit for acceleration. Since acceleration tells us how many meters per second the speed increases every second, we write this with the unit:
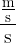
When we simplify the double fractions, we obtain the unit in the form:
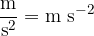
If the initial velocity 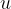 is
is 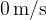 and the observed start time is
and the observed start time is 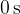 , then we can write the acceleration in a simplified form as:
, then we can write the acceleration in a simplified form as:
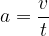
During uniformly accelerated motion, the velocity increases with time, so the final velocity is greater than the initial velocity. This means that the change (difference) in speed is positive. It follows that the acceleration is also positive.
If in the observed motion the change in time 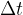 is equal to the final time
is equal to the final time 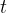 and the change in velocity
and the change in velocity 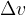 is equal to the final velocity
is equal to the final velocity 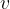 then acceleration:
then acceleration:
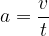
If we make 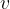 subject of the equation, we have:
subject of the equation, we have:
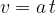
Acceleration tells us the increase in speed within the observed time interval:
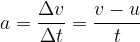
During uniformly accelerated motion, the acceleration is positive and independent of time (constant).
The current value of the speed (instantaneous speed) at any time 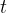 is calculated from the formula:
is calculated from the formula:
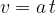
In the chapter, Uniform motion, we took a closer look at how to calculate the distance covered during uniform motion when the speed is constant.
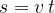
But, during uniformly accelerated motion, the velocity is not constant, so the calculation of the distance covered using the above equation would be incorrect.
How therefore do we solve this problem?
We first assume that the body is at rest at the beginning of the observation, and then accelerates uniformly for some time.
Because the velocity changes uniformly with time, we can increase the time interval of the observation without making a mistake. Instead of looking for the average speed by individual intervals, we can calculate the average speed for the entire observed time interval. This is called the average velocity of the whole journey of the train and is denoted by  .
.
The average speed of uniformly accelerated motion is the arithmetic mean of initial and final speed:
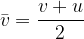
or, if the initial speed is 0, then the average speed is equal to:
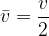
The average speed of motion is the speed at which an object would have to move uniformly in order to travel the same distance at the same time as in non-uniform motion.
When the initial velocity is zero, the average speed is calculated using the formula:
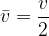
The formula for average speed takes into account that the body's speed changes. Therefore, we can calculate the distance travelled at an average speed in a similar way as with uniform motion:
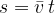
Let's look at the picture above. We focus on the red rectangle and the green triangle. The planes of both shapes are the same. We will see, however, that the planes of both shapes signify the distance travelled by the body in non-uniform motion.
Red rectangle
There is a point on the ordinate axis that represents the average velocity  . From the coordinate origin, draw a rectangle with sides of length
. From the coordinate origin, draw a rectangle with sides of length  and
and 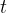 and calculate its area.
and calculate its area.
The area of a rectangle is equal to the product of length and width, i.e., 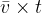 . According to the above formula, we can see that we have calculated the distance
. According to the above formula, we can see that we have calculated the distance  :
:
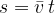
Green triangle
The triangle under the velocity-time graph also has exactly the same area. It is calculated using the formula of the area of triangle, so:
Therefore, it can be clearly seen that the distance travelled during uniformly accelerated motion can also be calculated by simply finding the area under a velocity-time graph.
With the help of the above formula, we can also draw a graph of the distance against time. We mark the times on the time axis (abscissa axis). For each selected time using the formula above, we calculate the distance  and enter it on the ordinate axis. We mark the points where the abscissas and ordinates intersect and connect them to make a curve.
and enter it on the ordinate axis. We mark the points where the abscissas and ordinates intersect and connect them to make a curve.
We have seen that the distance travelled during uniformly accelerated motion can be calculated in two different ways when the initial velocity is equal to zero. It can be calculated by:
multiplying the average speed and time,
finding the area under the velocity-time graph.
For uniformly accelerated motion (also applies to any non-uniform motion), the distance travelled is the area under the velocity-time graph.
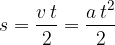
It can also be calculated as the product of the average speed and time:
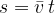
Graphs of uniformly accelerated motion with an initial velocity of zero
A: Velocity-time graph
The speed increases uniformly with time. This means that the speed increases equally every second. The graph is an ascending straight line. The distance of the body can be calculated by finding the area under the graph.
B: Acceleration-time graph
Acceleration does not change. The graph is a horizontal line. The slope is zero.
C: Distance-time graph
The body covers a longer distance every second as it moves faster and faster. The distance changes over time along a curve called a parabola.
What if the initial speed is not equal to zero?
The distance is calculated in a similar way as in the case where the initial speed is zero. Even in this case, the distance is equal to the area under the velocity-time graph. It can be calculated in two ways:
Calculating the distance using the average speed
The motion starts with the initial speed 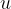 and then the speed increases uniformly to the final speed
and then the speed increases uniformly to the final speed 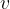 .
.
The average speed is:
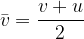
The whole distance, however, is the same as if it were moving uniformly at an average speed:
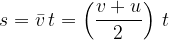
Calculating the distance using the area under the velocity-time graph
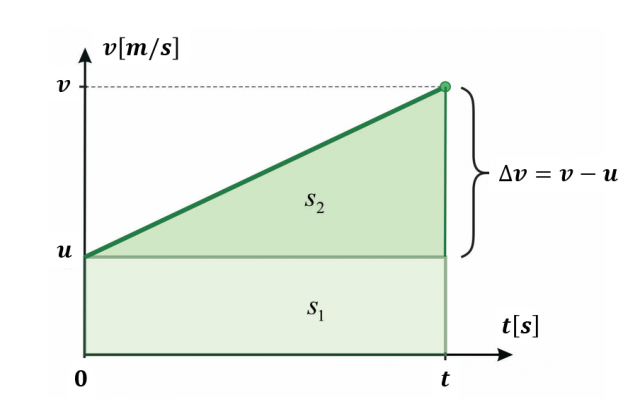
Calculating the distance using the area under the velocity-time graph when the initial speed is not zero
The distance is equal to the area under the velocity-time graph. From the picture we see that the figure on the velocity-time graph consists of two shapes:
rectangle,
triangle.
The area of the rectangle represents the distance that the body would cover if it moved uniformly at the initial velocity 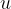 :
:
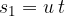
The distance that the body would cover during acceleration from the initial to the final speed is calculated using the area of the triangle:
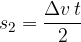
where:
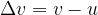
The total distance will be equal to the sum of the areas of both shapes:
In the event that the initial speed is not equal to zero during uniformly accelerated motion, the distance covered is calculated using:
the average speed:
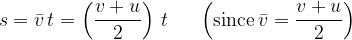
the formular:
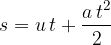
A body's speed can also drop uniformly over time. Such a motion is called a uniformly decelerated motion.
Let us calculate the acceleration for such a motion.
The acceleration has a negative sign. This is also called deceleration.
The distance is:
During uniform deceleration, the velocity decreases uniformly with time. The graph of the velocity against time is a descending straight line.
The acceleration is negative and constant. It is the quotient of the initial speed and the time taken.
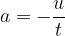
The distance covered is given as:
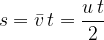
Graphs of uniformly decelerated motion.
A: Velocity-time graph
The speed decreases uniformly with time. The graph is a straight line with a descending (negative) slope.
The slope of the line represents the deceleration. It is also called negative acceleration.
The area under the velocity-time graph is the distance travelled.
B: Acceleration-time graph
Acceleration is negative and does not change over time. The graph is a horizontal line (parallel to the time axis).
In nature, motion is almost always complex. A car driver:
starts with acceleration,
drives uniformly for some time,
finally stops by braking.
Such motion can be divided into separate intervals. The duration of each interval is denoted by 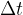 , as shown in the figure below.
, as shown in the figure below.
The average speed of the motion is the speed that the body would have:
if for the whole time 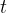 , it would move uniformly, and
, it would move uniformly, and
cover the same distance  as in the compound motion.
as in the compound motion.
The average speed in compound motion is calculated by dividing the total distance by the total time:

In compound motion, we divide the motion into intervals where the motion is accelerated, decelerated, or uniform. The distance in individual intervals is equal to the area of the figure within the interval below the velocity-time graph. The total distance travelled is:
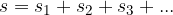
Average speed is the total distance divided by the total time:
