Personal collections


Archimedes (287 - 212 BC) was tasked by King Hieron to find out if the crown he had made was made of pure gold. He got the solution to the problem when he jumped into the water. He found that a body in water is as light as the weight of the water it displaced. By measuring the weight of the crown in air and in water, he calculated the density of the material from which the crown was made. From the calculated density, he found out what material the crown is made of.
He discovered the theorem about upthrust, which is also called Archimedes' principle after him.
Upthrust is a force that acts on a body in the opposite direction to its weight and is a result of the fact that the pressure in a liquid depends on the density 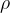 of the liquid and on the depth
of the liquid and on the depth 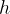 :
:
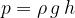
Since the body is located at different depths 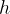 , the part of the body that is the deepest has the highest pressure (see Figure 1). The pressure gradually drops towards the part of the body that is closest to the surface of the liquid. Therefore, the forces on parts of the body that are at a greater depth are greater than the forces at a shallower depth.
, the part of the body that is the deepest has the highest pressure (see Figure 1). The pressure gradually drops towards the part of the body that is closest to the surface of the liquid. Therefore, the forces on parts of the body that are at a greater depth are greater than the forces at a shallower depth.
We think of the surface of the body as divided into small areas 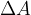 on which pressures
on which pressures 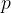 act. The result of pressure is a force:
act. The result of pressure is a force:
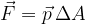
A body in the liquid is thus subjected to different compressive forces on the parts of the body immersed in the liquid (see Figure 1).
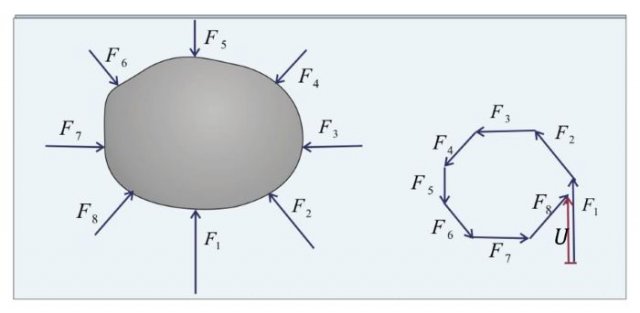
Figure 1: Upthrust is the resultant of forces caused by the pressure on the body
The resultant of the forces caused by the pressure on the body is the upthrust  and this is given as:
and this is given as:
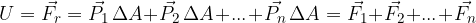
The upthrust can be greater than, equal to, or less than the weight of the body (see Figure 2):
When the upthrust is greater than the weight, their difference causes the body to rise until both forces are balanced - they become equal and oppositely directed. If it is a body in water, the body floats to the surface.
When the upthrust is equal to the weight, the body is at rest - e.g. floats in the water.
When the upthrust is less than the weight, the body moves downward in the direction of their resultant. If it is a body in water, the body sinks.
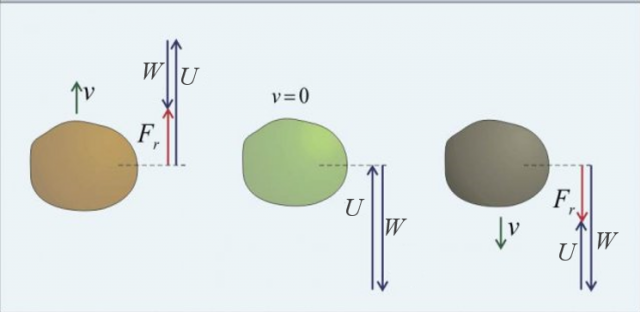
Figure 2: Upthrust is greater than weight (left), equal to weight (center) and less than weight (right)
Upthrust is the resultant of all the forces exerted by the pressure on a body in a fluid (liquid or gas).
It acts in the opposite direction to the weight of the body. A body immersed in a liquid is as light as the upthrust.
Let's imagine a cylinder with a base surface area 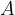 and a height
and a height 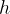 immersed in a liquid with a density
immersed in a liquid with a density 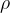 so that the axis of the cylinder is turned vertically upwards - Figure 3.
so that the axis of the cylinder is turned vertically upwards - Figure 3.
The force 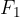 resulting from the pressure
resulting from the pressure 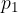 of the liquid at the lower surface of the cylinder is given as shown in figure 3, as:
of the liquid at the lower surface of the cylinder is given as shown in figure 3, as:
Similarly, we would get the equation for the force 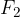 on the upper surface of the cylinder which is given as:
on the upper surface of the cylinder which is given as:
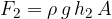
Pressure forces also act on the curved surface of the cylinder. Since they are perpendicular to the cylinder and in opposite directions, they cancel each other out. In Figure 3, the forces 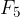 and
and 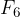 and the forces
and the forces 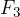 and
and 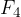 cancel out one another.
cancel out one another.
The resultant of the pressure forces is the upthrust  which is therefore given as:
which is therefore given as:
The factor on the right side of the equation is actually the weight of the liquid displaced by the cylinder. The equation applies to any body, not just a cylinder, but the proof is more complex.
The upthrust is equal to the weight of the fluid displaced by the body with its volume.
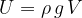
Two forces act on a body completely immersed in a liquid:
the weight, 
the upthrust,  .
.
Let us assume that the body has volume 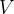 and density
and density 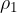 , and the liquid has density
, and the liquid has density 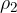 . When the weight and upthrust are equal, the body floats in water and then the body is in equilibrium:
. When the weight and upthrust are equal, the body floats in water and then the body is in equilibrium:
We have shown that the condition for a body to float completely immersed in a liquid is that the density of the liquid is the same as the density of the body.
If the density of the liquid is greater than the density of the body (and there are no other forces), the body rises. If the density of the liquid is less than the density of the body and there are no other forces, the body moves downward or sinks.
However, we can use an additional force (e.g. the force of the rope to which the body is tied) to balance all the forces so that the body remains at rest, even though the two densities are different.
The following applies to a body immersed in a liquid:
If the density of the liquid is equal to the density of the body, the body floats (rests) in the liquid.
If the density of the liquid is greater than the density of the body, the upthrust prevails and the body floats to the surface (moves upwards).
If the density of the liquid is less than the density of the body, the body sinks (moves in the direction of gravity).
With an additional force (e.g. the force of a rope) we can balance the body so that it remains stationary even if the density of the liquid is not the same as the density of the body
If the density of the body is less than the density of the liquid (e.g. water), the body floats to the surface. Part of the volume of the body, which would have displaced the liquid and thus caused the upthrust, now looks out of the liquid. The upthrust decreases until the forces are in equilibrium. Then the body rests on the surface of the liquid.
If the density of the liquid is less than the density of the body, the body sinks and settles to the bottom. In this case, the force of the base balances the weight of the body and the upthrust so that the sum of all forces is zero.
What if the body is e.g. cemented at the bottom of the sea? In this case, there is no upthrust or the upthrust is reduced, depending on the shape of the body and the size of the surface with which it is attached to the bottom. The condition for the upthrust is that the body is surrounded by liquid from all sides.