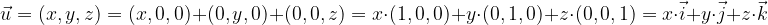Any vector in a plane (space) can be expressed in a single way as a linear combination of base vectors in a plane (space), where
the base of the plane consists of two arbitrary non-zero and non-parallel vectors (the plane is a two-dimensional space)
space is three arbitrary non-zero and non-parallel vectors (space is three-dimensional space).
If the vectors are drawn in a rectangular coordinate system in the plane, the base vectors are denoted by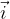 
and 
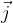as shown in Figure 1.
Figure 1
If a rectangular coordinate system is given in space, the base vectors are denoted by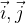 
and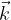 
as shown in Figure 2.
Figure 2
The following properties apply to the base vectors in the plane and space:
vectors are of length 1 unit (are unit vectors)
the pair is rectangular
vector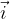 
has the same direction as the x axis, vector 
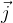has the same direction as the y axis, and vector 
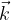has the same direction as the z axis, as shown in Figure 1 and Figure 2.
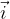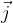The base of the plane is called the standard orthonormal base of the plane, which consists of two bases of the vector and with the following components:
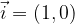
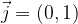
A similar space base is called standard orthonormal space base, and it consists of three base vectors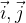 
and 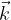with the following components:
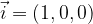
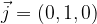
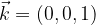
Vectors in a rectangular coordinate system in a plane (or space) are usually drawn by selecting the starting point of the coordinate system as the starting point. Such vectors are called local vectors.
The local vector of the point A is a vector with a starting point in the coordinate origin, and its end point is just the point A. We denote it by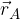 
, and its components are equal to the coordinates of the point A.
All rules and formulas that apply to vectors with two components also apply to vectors with three components, ie vectors in a rectangular coordinate system in space.
The vector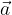 
with components 
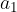and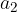 
and the vector 
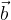with components 
and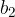 
are summed by adding the same components.
Vector
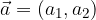
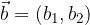
we add by adding their components:
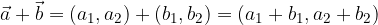
The vector 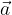with the components 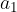and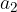 
is multiplied by a number (scalar) by multiplying the individual component of the vector by this number (scalar).
Given vectora:
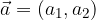
multiply by a real number k by multiplying each of its components by a real number k:
Before deriving the length of the vector, let us recall Pythagoras' theorem, which says that in a right triangle, the square on the hypotenuse (c) is equal to the sum of the squares on the other sides (a and b):
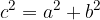
Now in the rectangular coordinate system in the plane we draw the vector 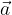with the starting point in the origin, and the components 
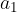and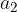 
as shown in Figure3.
Figure 3
The length of the vector 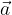is exactly the hypotenuse of a right triangle, and the components of the vector 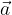are its sides.
The formula for calculating the length of the vector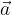 
with components 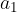and 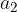, derived from the Pythagorean theorem, reads:
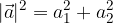
or, if we express the length of the vector:
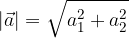
where 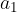is the first component of the vector (section on the x axis) and 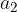is the second component of the vector (section on the y axis).
The components of a vector with any starting point A and any end point B are obtained by subtracting the local vector of the starting point from the local endpoint vector (which has components equal to the coordinates of the point B and coordinates of the point A.
Any points A and B given by the local vectors 
and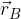 
are given. The components of the vector 
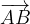are calculated:
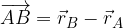
The local vector of the point S, which is the midpoint of the line AB is equal to half the sum of the local vectors 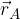and we calculate .
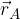If S is the midpoint of the line AB, then the local vector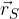 
is equal to:
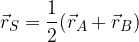
The components of the local vector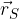 
are at the same time the coordinates of the point S.
Any vector
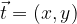
in the plane can be expressed by base vectors
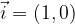
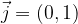
in two ways:
Any vector expressed by base vectors, first mode
The first way is to multiply the first component of the vector by the base vector 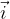and the second component by the base vector 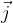, which means that the vector 
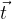with the components (x, y) is expressed as:
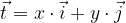
Any vector expressed by base vectors, second mode
Another way is to expresse the components of the vector to the components of the base vectors, which means that the vector 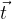with the components (x, y) is expressed as:
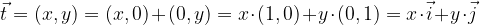
In a similar way, any vector
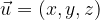
in space can be expressed by base vectors
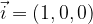
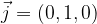
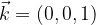
in two ways:
First way for any vector to be expressed by base vectors
The first way is to multiply the first component of the vector by the base vector 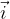, the second component by the base vector 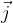and the third component by the base vector 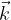, which means that the vector 
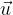by the components (x, y, z)
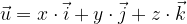
Second way for any vector to be expressed by base vectors
Another way is to parse the components of the vector to the components of the base vectors, which means that the vector 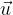with the components (x, y, z) is expressed as:
