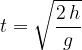Personal collections


The Earth attracts us with a force, which we call gravity or gravitational force. If we stand on the ground, we feel the weight with which we act on the ground and the force with which the ground acts on us.
What if we jump off a plane?
In this case, however, we do not have a floor under our feet to hold us, so we move because of the weight. This movement, as long as the air resistance is negligible, is called a free fall.
What if two differently heavy friends jump out at the same time? Will they fall just as fast? We wonder if the speed of fall depends on mass. Let's do a simple experiment.
Due to the speed of fall, it is not possible to determine with the naked eyes what this motion is. At times, even measurements to investigate the laws of free fall were also very difficult. The problem was inaccurate instruments for measuring short times.
As a result, many believed that free fall was a steady movement. Today we know that this is uniformly accelerated motion with the acceleration we will determine below.
In this chapter, we will learn how to calculate the speed, distance, and time of a body’s fall. In doing so, we will neglect the influence of air resistance.
Today, observing falling bodies is much easier than in older times. We have fast and accurate instruments for measuring time and speed. We can also help ourselves with a camera or camcorder. Thus, a free fall can be observed during slow-motion playback.
Let’s experiment with a tennis ball and calculate its acceleration at free fall.
The resulting acceleration is the free fall acceleration or gravitational acceleration. Let us denote it by 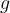 . The more accurate value of gravitational acceleration is:
. The more accurate value of gravitational acceleration is:
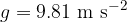
The value of the free fall acceleration above applies only to the fall on the surface of the Earth planet. Accurate measurements would show that this acceleration varies even slightly in different parts of the Earth. If we rise above the Earth's surface with a spacecraft, the acceleration of free fall will be smaller.
Each celestial body has a different gravitational acceleration. However, the following applies:
the greater the mass of a celestial body, the greater its gravitational acceleration,
the more we move away from the celestial body, the smaller the acceleration of free fall.
Free fall is a uniformly accelerated motion. The acceleration of free fall is:
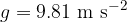
Let's round it to the nearest whole number:
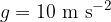
The free fall is therefore uniformly accelerated motion with an initial velocity of zero. We assumed that we were just dropping the object to fall freely. However, if we throw it down, we must also consider the initial speed.
All the findings and equations we learned in the chapter Uniformly accelerated motion also apply to free fall, as it is the same motion. We will only change some parameters:
Instead of the distance  we will write height
we will write height 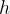 .
.
Instead of acceleration 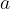 we will write acceleration due to gravity
we will write acceleration due to gravity 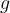 .
.
In the tasks we will take an approximation for acceleration due to gravity:
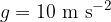
In the calculations, we will use a velocity-time graph.
The speed increases uniformly with time. It increases by  every second. The instantaneous speed is calculated by the equation:
every second. The instantaneous speed is calculated by the equation:
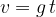
The object falls to the ground during time 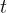 . Just before it falls to the ground, its speed is at its highest. We call it final velocity and denote it by
. Just before it falls to the ground, its speed is at its highest. We call it final velocity and denote it by  :
:
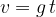
In the chapter Uniformly Accelerated Motion, we learned that the distance (height of fall 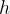 ) is equal to the area of the figure below the velocity-time graph. In our case, this is the shaded part of the graph above. However, it can also be calculated with a known average speed of fall.
) is equal to the area of the figure below the velocity-time graph. In our case, this is the shaded part of the graph above. However, it can also be calculated with a known average speed of fall.
Calculating the height of fall using the average speed
The height of fall  is the average speed
is the average speed 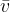 of fall multiplied by the time
of fall multiplied by the time 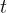 of fall:
of fall:
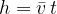
The average speed is given as the final speed  divided by 2 since the initial speed
divided by 2 since the initial speed 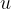 is zero:
is zero:
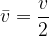
Therefore:
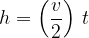
Calculating the height of fall using the area of the figure below the velocity-time graph
The height of fall is the area of the triangle:
From the given height  , we can calculate the fall time
, we can calculate the fall time 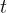 . We start from the equation for the distance (height):
. We start from the equation for the distance (height):
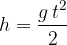
Let's obtain the expression for the fall time 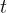 from the formula above:
from the formula above:
Using the obtained equation, we could also calculate the final velocity  at a given height of fall:
at a given height of fall:
Let's look at an example where we calculate the time of fall from a given height.
The speed of fall  at a given fall time
at a given fall time 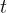 is calculated by the equation:
is calculated by the equation:
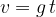
The speed of fall  at a given height of fall
at a given height of fall  is calculated by the equation:
is calculated by the equation:
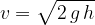
The height of fall  at a given fall time
at a given fall time 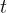 is given as:
is given as:
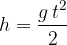
The fall time 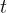 at the given fall height
at the given fall height  is given as:
is given as: