Vieta's formula is obtained by equating the general form of the quadratic equation
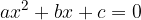
where a, b and c are the coefficients of the quadratic equation (which are arbitrary real numbers) and the vertex form of the quadratic equation:
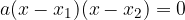
where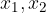 
are the solutions or roots of the quadratic equation.
The Viet formulas are the formulas that give us the relationship between the coefficients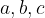 
and .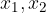
We equate the general and zero form of the quadratic equation and find the relation between the coefficients of the quadratic equation and their zeros:
Let's derive the equation:
We get the Viet's formula which is the relationships between the coefficients of the quadratic equation and their solutions:
