Wave on the surface of a liquid, e.g. water is a unique form of a wave that is neither transverse nor longitudinal. It is caused by the gravitational oscillation of water particles, similar to how a simple or string pendulum oscillates.
The source of the wave can be a one-off disturbance (a stone thrown into the water), the source can be:
wind,
a ship,
an earthquake, or
for example, arbitrary periodic oscillation of the water surface.
Waves move away from the wave source at a speed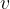 
. Similar to longitudinal, transverse, or light waves (electromagnetic waves), waves on a liquid are also reflected and diffracted at obstacles. They can be refracted, similar to light if the speed of the wave changes - e.g. due to the change in water depth.
If there are several sources of waves, the waves add up (interference of waves). A stationary wave can even occur, e.g. between an island and the coast, when the amplitude of the waves doubles due to the constructive interference of the incident and reflected waves; even large ships can get into trouble because of this phenomenon. We can also study the Doppler effect in water when the source of the wave (ship) is moving towards a stationary observer or an observer on a boat towards a traveling wave, etc.
All these phenomena can be easily observed and studied in liquids. The knowledge can then be transferred to other types of waves.
A ship on the Ljubljanica is a source of waves. The waves bounce off the shore so that the incident and reflected angles are the same
The basic terms explained in the chapter, sine transverse waves also apply to the case of waves through a liquid. The only difference is that the water particles do not oscillate transversely, but move along a circle, ellipse, or some other curve, depending on many parameters that are difficult to capture mathematically.
The derivation of the wave velocity equation is one of the more difficult tasks of hydrodynamics. Here we can summarize the derivation results for two cases: shallow water and deep water.
When shallow, the water depth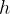 
is much smaller than the wavelength 
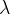. In this case, the wave speed 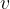is given as:
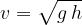
The wave speed in shallow water therefore depends only on the depth 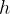and the gravitational acceleration 
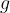. However, in deep water, when the depth 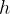is much greater than the wavelength 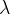, the wave speed 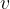is given as:
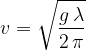
In deep water, the wave speed depends on the gravitational acceleration 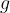and the wavelength .
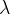The wave speed 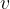in shallow water is given as:
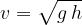
The wave speed 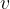in deep water is given as:
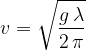
Waves are approximately sinusoidal only if the wavelength of the wave is large compared to the amplitude and if the water depth 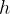is much greater than the wavelength 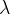. In this case, we can consider the water particles to be circulating, as shown in Figure 1 below.
Rotation of water particles in a sine wave
The speed of rotation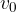 
of water particles depends on the angular speed 
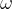and the radius of rotation which is equal to the amplitude 
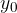of the wave, so we can write:
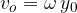
The angular velocity 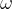is given as:
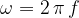
The frequency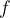 
and the wavelength 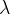are related by the equation:
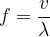
The rotation of water particles causes, for example, a swimmer to swim faster in the direction of travel of the waves and slower against the waves.
Unlike a transverse wave on a tensioned rope, a wave on water can propagate in all directions. The direction of wave propagation in water is shown by the wave beam. Let's mark it with an arrow. The crest or trough of a wave is schematically illustrated by a wave line (also called a wavefront). The distance between two wave lines is the wavelength.
The direction of the wave beam and the shape of the wave line depend on the shape of the source. If the source of the wave is pointed, the wave propagates in the form of concentric circles, as shown in the figure. The wave beam goes radially from the centre of the circle, where the source of the disturbance is, the wave lines are the concentric circles that move away from the centre of the circle:
Circular waves
For a better representation, the wave beam (arrows) and wavefronts (concentric circles) are drawn in the figure below:
Circular waves with marked wave beams and wavefronts
If the source of the wave is e.g. a long straight rod with which we create a disturbance on the water, creating straight waves. The wave lines are straight lines, and the wave beam is perpendicular to the wave lines and shows the direction of the wave.
The bow of a ship pushing water creates roughly straight waves. Ridges are visible - wave lines, a wave beam goes perpendicular to the wave lines, indicating the direction of wave movement
For a better representation, the wave beam (arrows) and wavefronts (concentric circles) are drawn in the figure below:
Waves and wave beam drawn in the figure
