Personal collections


The number a is the zero of a polynomial when the value of the polynomial at this point is equal to 0.
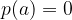
In this case, the polynomial p (x) is divisible by the linear polynomial x-a.
The value a is a zero polynomial
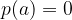
when dividing a polynomial by
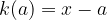
we get the expression of the form
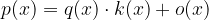
and the remainder R(x) is zero:

A polynomial of the nth degree has at most as many zeros as its degree.
A polynomial of degree n can have repeated zeros.
Any arbitrary n-degree polynomial can be written as the product of linear polynomials. This is due to the basic theorem of algebra.
The basic theorem of algebra says that every nonconstant polynomial with complex coefficients has at least one complex zero.
In polynomials with real coefficients, complex zeros always occur in conjugated pairs:
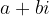
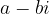
The consequence of the basic theorem of algebra is also a statement: any inconsistent polynomial with real coefficients can be split into real numbers in the range of
product of linear polynomials OR
product of linear polynomials and non-splitting square polynomial.
Linear polynomials give us zeros with real coefficients. While the solutions of each uncleaved square polynomial are two conjugate complex zeros. Let’s look at this in a practical example.
Every inconstant polynomial of odd degree has at least one real zero.