We turn a bicycle upside down so that it stands on the balance and the seat. We grab the front wheel and turn it with a jerk of the hand. The wheel, which is initially at rest, begins to rotate with a certain angular velocity after the impact of our hands. During the rotation, all points on the circumference move with uniform acceleration.
If we grab the wheel a bit closer to the axis of rotation instead of at the rim, rather at the tip (see Figure 1), we would need a slightly higher force to produce the same final angular velocity. This makes us think that we need the torque of a force for a certain speed of rotation of the wheel. We cause the torque with the force of our hands; in this case, the lever is equal to the distance between the force and the axis of rotation.
With the application of torque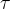 
of a force, with which we act on the system for a certain time 
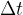, we change the speed of rotation of the wheel. We say that we have changed the angular momentum 
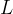with the torque of the force.
Figure 1: We turn the wheel with a torque
In this chapter, we will learn about two new physical quantities that are closely related:
moment of inertia, and
angular momentum.
The moment of inertia has similar importance in angular momentum as the mass in the case of a linear momentum. Due to mass, a body persists in motion if no force acts on it. The same applies to the moment of inertia in rotation: a body persists in rotation if no torque acts on it.
Let's first learn about the moment of inertia of a point-like body moving around a circle of radius 
. We then extend the knowledge from this simple example to a rotating rigid body.
Two forces act on a point body that rotates with uniform acceleration (Figure 2):
Figure 2: Forces in uniformly accelerated rotation
The centripetal force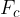 
, which is the force that keeps the body in rotation. It is equal to the product of the mass 
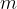and the centripetal acceleration 
:
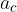where the centripetal acceleration is given as:
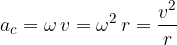
Since the angular velocity changes with time (the body rotates with uniform acceleration), the centripetal acceleration also changes with time; if the angular velocity increases, the centripetal acceleration also increases.
The second force is the tangential force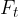 
and according to Newton's second law, it causes the body to move with tangential acceleration (linear acceleration) 
:
The expressions we obtained are also called Newton's second law for circular motion.
Let's write the relationship between force and acceleration (Newton's second law):
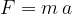
We replace force 
with torque 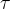, mass 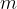with moment of inertia 
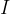and acceleration 
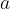with angular acceleration 
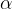, and we get:
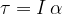
The torque of a force on a rotating point body causes the body to move with an angular acceleration 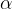. The proportionality factor is the moment of inertia :
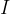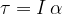
Here, the angular acceleration 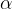is the quotient of the tangential acceleration 
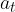and the radius :
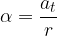
The moment of inertia of a point body is:
Let us take any rigid body rotating about any axis as shown in Figure 3.
Figure 3: Moment of inertia of a rigid body
The body is divided into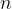 
small cubes with mass 
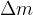. The squares are distant from the axis of rotation by different distances .
The first cube has its moment of inertia as:
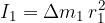
second cube:
and any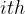 
cube:
The moment of inertia of the whole body is equal to the sum of the moments of inertia of individual cubes:
The moment of inertia of a rigid body is the sum of the moments of inertia of the parts of the body at a given axis of rotation:
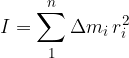
Let's also write down the moments of inertia of some other geometric bodies:
We already mentioned in the introduction that torque lasting a certain time 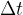changes the angular momentum of the body. But we didn't say what the angular momentum is.
Let's write again the relationship between torque 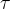, moment of inertia 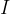, and angular acceleration :
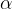We therefore define the angular momentum 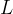as the product of the moment of inertia 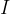and the angular velocity 
:
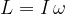
The angular momentum is a vector. We will write it as a scalar, noting the sign:
Counter-clockwise rotation gives a positive torque.
Clockwise rotation gives a negative torque.
The angular momentum 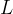is the product of the moment of inertia 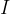and the angular velocity :
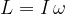
The angular momentum is positive if the body rotates counterclockwise and negative if it rotates clockwise.
Angular momentum and linear momentum are related concepts and complement each other. If the linear momentum is calculated for bodies that move translationally (e.g. along a straight line), the angular momentum is calculated for bodies that rotate around a given axis.
Let's write again the equation:
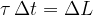
The term on the left is called the angular impulse, and on the right is the change in momentum:
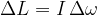
The written equation above is called the conservation of angular momentum.
If we act on a body that can rotate around a selected axis with an angular impulse, we change its angular momentum.
If there is no external angular impulse, the angular momentum is conserved:
If there is no external angular impulse, the angular momentum is conserved:
