For the introduction, we ask ourselves the question: Does the air pressure depend on the speed of air-wind movement? The answer is yes. When the wind blows into the streets, e.g., between the city’s skyscrapers, the speed increases and the pressure decreases. This is somewhat surprising, as it contradicts our experience: the greater the crowd in the street, the more people struggle, the greater the pressure between them.
This law is described by Bernoulli's equation. In this material, we will derive it with the help of the energy equation:
We are aware that the above equation applies only to a rigid body (a body that does not deform under the influence of force). This does not apply to liquids, so we expect the derived equation to be quite inaccurate in reality. For the equation to be valid at least approximately, we need to provide some conditions.
Bernoulli's equation is therefore derived under the following assumptions (unknown terms are explained below):
the flow of liquid (liquid or gas) is laminar;
ignore the compressibility of the liquid (gas);
the fluid does not heat up during movement due to an external source of heat;
friction between liquid molecules (viscosity) and between the pipe and the liquid is negligible
Molecules of liquids move along tracks called currents. Currents are limited by the current pipe. These are the boundary currents within which we observe the current. An example of current pipes, with a marked current pipe, is shown in Figure 2:
Figure 2: Currents and current pipe
Dense currents mean faster flow. The flow is faster when the cross-sectional area of the pipe is smaller.
But before we write down Bernoulli's equation, let's first get to know the following concepts:
laminar and turbulent flow,
stationary flow,
liquidity of liquids.
According to the tracks of motion, we distinguish between laminar and turbulent flow (Figure 3).
Figure 3: Laminar and turbulent flow
In laminar flow, currents flow side by side; they do not swirl, the molecules do not collide with each other, and do not interfere with movement - Figure 3, left.
If the tube has the same cross-sectional area everywhere (as in Figure 3), the velocity of the molecules on each current is also the same. However, the speed between the currents can vary. It is smaller at the edge of the pipe than in the middle. The cause is viscosity-friction between the pipe and the liquid and between the liquid molecules. In deriving Bernoulli's equation, we will ignore this difference.
In the case of eddy or turbulent flow (Figure 3 - right), the currents are irregular in shape and change constantly over time. The current indicates the direction of the liquid particles at the selected time. The very next moment, the current changes, and the direction of particle movement also changes.
Stationary current is a current in which the velocities of particles (at any observed point) along the current do not change with time.
For the current to be stationary, two conditions must be met:
volume flow must be constant;
current must not be turbulent.
At steady flow, the velocity vector of liquid particles does not change with time. The condition for this is that the volume flow is constant and that the liquid does not swirl.
Let us take a closer look at both conditions:
Volume flow is constant
Let us remember that the volume flow tells us how much volume of liquid flows through the selected cross-section of the pipe in a given time. Let us write this down:
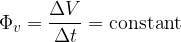
The equation for constant volume flow can also be written in the form:
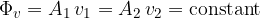
where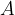 
is the cross-sectional area through the flow and 
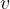is the velocity of the fluid through that cross section.
The flow constancy does not depend on the laminarity or turbulence of the flow itself or the viscosity of the fluid. The above equation applies in all these cases, except that we must consider the average particle velocities through the selected cross section:
Figure 5: River flow. In the strait in the background, the flow is faster and turbulent
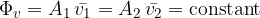
Current is not turbulent
This condition applies by definition: in a stationary flow, the velocities of the particles do not change, which is not true for turbulent flow.
The cause of viscosity is internal friction between liquid molecules. Take the example of a moving fluid in a pipe - Figure 3, left. Its maximum speed is in the middle of the pipe. Through internal friction in the fluid, velocity is transferred from the faster layer to the slower one. Layers of liquid travel at different speeds along the entire cross-section. The layer of liquid located right next to the pipe sticks to the pipe, and its velocity is zero.
Friction between fluid particles is performed by negative work and smaller kinetic energy of moving fluid.
The viscosity is described in more detail in the material Viscosity.
Viscosity describes the internal friction between particles of a moving fluid. Due to the influence of viscosity, the current is fastest in the middle of the pipe and drops to zero right next to the pipe.
The Bernoulli equation relates the pressure and velocity of fluid particles in a pipe where an ideal fluid flows. The ideal liquid is:
incompressible and
has a viscosity of zero.
Since there is no internal friction between the liquid particles (viscosity is zero), the liquid will also not heat up. Assume that there is also no external source of heat or that the pipe is in a thermally insulated vessel. The flow should be laminar.
The ideal liquid is an incompressible liquid with a viscosity of zero.
Let us derive Bernoulli's equation. We help ourselves with a sketch of an inclined tube as shown in Figure 7 below:
Figure 7: Derivation of Bernoulli's equation
On the left side of the piston, with the force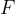 
, we act on the surface with the plane 
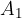. This creates pressure:
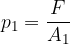
Due to the action of force, the piston and the fluid under the piston move at a speed of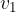 
by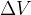 
. The center of gravity of this part of the liquid should be at the height 
.
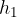For the same volume, the liquid in the lower, narrower part of the pipe also moves, as the liquid is incompressible. The observed section is at the height of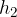 
. The speed 
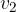is greater than 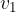, since the equation for the constant of the volume flow applies:
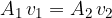
What is the pressure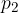 
?
We start from the energy equation: work pressure is equal to the change in kinetic and potential energy:
We got the Bernoulli equation. The terms in the equation are:
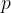is static pressure;
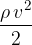is the dynamic pressure or kinetic energy density;
is the potential energy density.
Bernoulli's equation says: In an ideal fluid, the sum of static pressure, dynamic pressure, and potential energy density inside the flow tube and along the flow tube is constant. If these quantities are observed in two places, the following applies:
The higher the kinetic energy (velocity) and (or) the potential energy (height), the lower the pressure.
In a riverbed is a rectangular block, e.g. bridge girder (Figure 9). The block represents an obstacle in the path of the water. The plane set by the current has a cross-sectional area 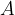. Far in front of the obstacle is the river with speed 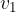and the pressure 
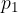of the moving water. Hydrostatic pressure is neglected. When a stream of water hits an obstacle, it stops next to it. The velocity of water perpendicular to the obstacle or the density of kinetic energy is zero here, and the pressure is 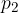. The difference 
between the two pressures is called the static pressure. The force with which the block impedes the flow, however, describes the quadratic law of resistance.
On the other side of the obstacle, the water swirls and drains forward.
Figure 9. Water flow encounters an obstacle
Let's write Bernoulli's equation:
The force with which the current acts on the obstacle is calculated from the static pressure and is given as:
The same force, only the opposite, is the force with which the obstacle obstructs the flow. We call it the force of resistance:
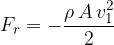
The written equation is not accurate. In our case, we took, as an obstacle, a block with a rectangular cross-section. What the actual resistance force is depends on the shape of the obstacle. It is enclosed in the factor 
, which represents the coefficient of resistance:
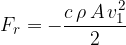
The equation is called the quadratic law of resistance. In the equation, 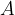is the cross-sectional area of the obstacle hit by the current, and is the resistance coefficient.
The table below gives the coefficient of resistance for some obstacle shapes.
The static pressure is the overpressure that occurs at the part of the obstacle at which the current hits, and therefore, the current velocity drops to zero there. The static pressure is calculated by the equation:
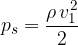
The quadratic law of resistance is described by the equation:
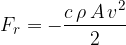
where:
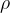is the density of flowing fluid,
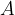is the cross-sectional area of the obstacle perpendicular to the flow direction,
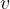is the speed of current flow away from the obstacle,
is the coefficient of resistance depending on the shape of the obstacle.
