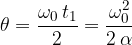Personal collections


Let's imagine a small body on a circular plane. The body is initially at rest but then begins to move with uniform acceleration. The tangential speed  of the body increases with the acceleration, which is directed in the direction of the tangent to the circle at every moment. We call it tangential acceleration.
of the body increases with the acceleration, which is directed in the direction of the tangent to the circle at every moment. We call it tangential acceleration.
Tangential acceleration can be directed in the direction of the body's motion. Then the speed of the body increases (Figure 1, left):

If it is directed in the opposite direction to the body motion of the body, its speed decreases (Figure 1, right):
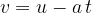
In addition to tangential acceleration, we also have radial (centripetal) acceleration  , similar to uniform circular motion. This is directed towards the centre of rotation and forces the body into a circular motion track.
, similar to uniform circular motion. This is directed towards the centre of rotation and forces the body into a circular motion track.
In uniformly accelerated rotation, the body moves in a circle with tangential acceleration 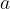 given as:
given as:
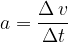
In a uniformly accelerated circular motion, the angular velocity 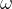 is no longer a constant. It varies with angular acceleration
is no longer a constant. It varies with angular acceleration 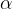 :
:
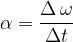
Let's use the equation from uniform circular motion, which connects the angular and tangential velocities :
The angular acceleration 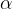 is the change in the angular velocity with time:
is the change in the angular velocity with time:
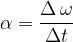
The tangential and angular accelerations are related by the formula:

From the material, Uniform circular motion, we recall the connection between the angle  described by the radius as the body travels in a circle and the angular velocity
described by the radius as the body travels in a circle and the angular velocity 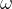 :
:

Analogously, in the material, Uniform motion for A-Level, we have a connection between the distance  , the speed
, the speed 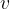 and time
and time 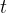 :
:
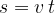
What if the angular velocity changes uniformly with time?
We have a similar case in the material, Uniformly Accelerated Motion for A-Level. In the material, we discussed the situation in which the speed changed uniformly with time and we calculated the distance as the area under the graph of the speed 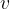 against the time
against the time 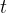 . We can use all the equations we learned in the material. We only change the notations:
. We can use all the equations we learned in the material. We only change the notations:
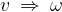
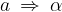
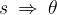
Let's consider the case where the angular velocity increases uniformly from 0 to the final value  .
.
The angular velocity changes with time according to the equation:
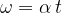
It attains the final value in time 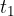 :
:

The area under the graph 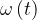 above is therefore given as:
above is therefore given as:
The angular velocity is initially zero. At time 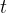 , it begins to increase uniformly with the angular acceleration
, it begins to increase uniformly with the angular acceleration 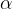 . The angle described by the line between the body and the centre of the circle is therefore given as:
. The angle described by the line between the body and the centre of the circle is therefore given as:
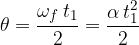
A body on the circumference of a circle has an initial angular velocity 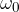 . At time
. At time 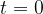 , its angular velocity begins to decrease uniformly with an angular acceleration
, its angular velocity begins to decrease uniformly with an angular acceleration 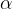 .
.
When does the body stop?
At time 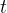 , the angular velocity
, the angular velocity 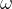 is:
is:
Let's also check the angle at which the body stops.
The angle  described by the body at time
described by the body at time 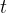 while stopping is given by the area under the graph
while stopping is given by the area under the graph 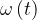 (see Figure 4):
(see Figure 4):
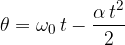
The body stops at an angle  which is given as:
which is given as:
The body rotates around the circumference of the circle at an angular velocity 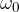 when it begins to stop at the time
when it begins to stop at the time  . The angle described in time
. The angle described in time 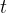 while stopping is given as:
while stopping is given as:
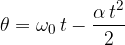
The body stops at the time:
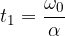
The total angle described by the body during stopping is given as: