Many natural phenomena repeat themselves at certain time intervals. Let's look at some of these recurring phenomena.
Let's observe the wheel at the amusement park.
The amusement park wheel rotates and the cabins rotate around the axis of rotation of the wheel
The entire wheel together with the cabins rotates around the axis. Cabins on the circumference of the wheel are said to rotate around a circle. This circle has a radius equal to the distance between the cabins and the axis of rotation in the middle of the wheel.
The phenomena described represent a curved motion called rotation. However, we must distinguish between two physical phenomena:
rotation,
revolution.
A body rotates as a whole. It rotates around a straight line that is stationary. This line is called the axis of rotation.
But if we observe individual points on a rotating body, we say that they are revolving since they move along a circular track with the centre in the axis of rotation. The radius of rotation is equal to the distance between the circle and the axis of rotation.
In the following, we will learn about the period, tangential speed, and frequency of rotation. We will also know and name the force that forces the body in a circular track.
Revolution is an example of curved motion, as the body moves along a curved track, a circle with radius 
.
If we place the body on a circular track and let it move uniformly, we notice that after a certain time, it returns to its initial position. The time required for the body to return to the starting point after completing a circular path is called the period of rotation. We denote it by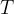 
. We say the body makes one revolution (round trip) during this time.
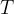The period of rotation is the time taken by a body in orbit to travel a circle of radius . It is denoted by , and the unit is second (
).
More often than the period of rotation, in physics and engineering, we use a physical quantity called the frequency of rotation. Frequency tells us how many times a phenomenon repeats itself in the observed time.
It is used in all repetitive (we call them periodic) movements: rotation, oscillation of weights on a string, oscillation of a guitar string, waves in the sea, alternating electric voltages, radio waves, etc.
Frequency and period of rotation are mutually dependent quantities. The more times the body rotates about the axis in the observed time, the less time it spends on one revolution. In other words, the higher the frequency, the lower the period of rotation.
The frequency of rotation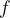 
is therefore inversely proportional to the period 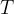. It is denoted by .
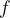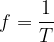
The unit for frequency is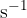 
. We also call it Hertz and it is written as 
.
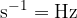
We can also observe the number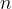 
of revolutions made by the body in any observed time interval 
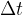. In this case, we calculate the frequency of rotation 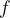using the formula:
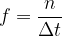
The frequency 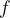is equal to the inverse of the period 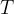. It tells us how many revolutions per second the body makes while rotating or revolving. Its unit is 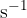or (Herz).
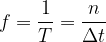
An object moves uniformly in a circle with radius . The distance between the object and the centre of the circle during rotation describes an angle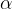 
. The distance 
travelled by the body along the circle in a certain time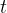 
is equal to an arc length of the circle with radius and is therefore given as:
Motion on a circle
The speed of rotation is called the tangential speed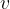 
. We calculate it in the same way as we calculate the speed in linear uniform motion:
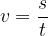
We can calculate the speed by taking the entire circumference of the circle as the distance and the time 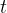will therefore be the time the body takes to make one complete revolution which is equal to the period .
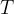Let's derive the formula for the tangential velocity from the formula above:
The higher the orbiting radius and the lower the period of rotation 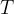, the higher the speed of rotation.
Let's write the speed of rotation in another form:
The tangential velocity is the speed at which an object moves in a circle.
Newton's first law states that a body moves uniformly and in a straight line if the resultant of all forces acting on it is equal to zero.
In uniform rotation, the object moves uniformly but not in a straight line.
The path of an orbiting body is a curved line - a circle. Therefore, a force must act on the body that forces it to change direction every moment and follow a circular path. This force is called centripetal or radial force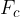 
. It works in a radial direction from the object, towards the centre of the circle.
Centripetal force allows the body to rotate on a string
With an experiment, we can determine what the centripetal force on a body on the string depends on. For this purpose, we take an electric motor whose frequency of rotation can be changed. We attach a rotating body of mass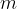 
, which can slide on a horizontal surface without friction, to the axis of the motor via the string of a spring balance.
Measurement of centripetal force with a spring balance
The spring balance directly measures the centripetal force. By varying the frequency of rotation of the motor, mass, and radius of rotation, we can investigate what the force depends on. The findings are as follows:
the centripetal force is higher if the mass of the body is higher,
the centripetal force is higher at a higher frequency of rotation,
the centripetal force is higher if the radius of rotation is higher (at the same frequency of rotation).
So far we have learned about the force of the string on which the rotating body is suspended. The string provides centripetal force and thus rotation. If the string were to break during the rotation, the body would continue its path in the direction of the speed it has at that moment. It is straight, in the direction of the tangent to the circle.
In addition to the string, there are other forces that make the rotation. For now, let's mention just two:
frictional force,
gravitational force.
