In the material, light waves, we learned that light is an electromagnetic (EM) wave. As with any wave, the EM wave of light is also characterized by wave phenomena:
diffraction,
interference.
In this material, we will focus on the diffraction of light on a diffraction grating.
A diffraction grating is a device that has a large number of parallel slits on which light, just like sound, diffracts. The light waves emerging from the slits of the diffraction grating can be added (amplified) or subtracted (attenuated) in certain directions. The amplified waves are called the maxima while the attenuated waves are the minima. The phenomenon is called interference. The direction of amplification or attenuation depends on the density of the slits in the grid, as well as on the wavelength, i.e. the colour of the light.
If we focus on a diffraction grating with white sunlight, which contains all visible colors, we can get a rainbow on the diffraction grating screen.
Figure 1: Diffraction of white light on the diffraction grating
With the help of a diffraction grating, we can determine which colours are represented in the spectrum of the emitted light and also measure their wavelength.
The diffraction grating consists of a large number of slits through which light passes.
Figure 2: Diffraction grating
The slits must be narrow compared to the wavelength of the incident light - Figure 2:
The density of the slits of the diffraction gratings varies widely, from several hundred to several thousand slits per millimetre. Also, the height of the diffraction grating or the total number of slits that the diffraction grating has is different. It is determined by the constant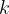 
called the grating constant. It tells how many slits the grating has per unit length. The grating constant and the grating spacing 
are inversely proportional:
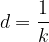
Let's take a diffraction grating with a distance between two adjacent slits and let the light of wavelength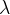 
fall perpendicularly on the grating.
Similarly, as in the case of sound interference, we consider also in the case of light waves that each slit in the grating is a Huygens source radiating hemispherical waves. The condition is that the slit is narrower than half the wavelength of the incident light - see the Huygens principle described in the material Diffraction and interference of sound.
Waves are amplified in a direction where the path difference between waves traveling through two adjacent slits is equal to a multiple of the wavelength - see Figure 3.
Figure 3: Light amplification: left image N = 1 (first-order maxima), right image N = 2 (second-order maxima)
From Figure 3, we can see that the waves are amplified in the direction when:
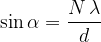
If:
N = 0, we get an undiffracted light,
N = 1, we get the first-order maximum,
N = 2, we obtain the second-order maximum.
What is the maximum possible order number 
of the maxima? The maxima of the maximum possible order number can occur at an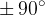 
. We know that:
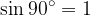
It implies that:
A diffraction grating amplifies light of wavelength 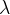in the direction 
if:
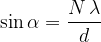
where is the grating spacing and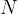 
is the order number.
The maximum possible order number is given by the equation:
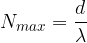
Waves attenuate in directions where the path difference is equal to 
of the wavelength, 
of the wavelength, ... or in general:
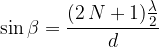
In this case, the waves emanating from two adjacent slits are subtracted - the wave is weakened.
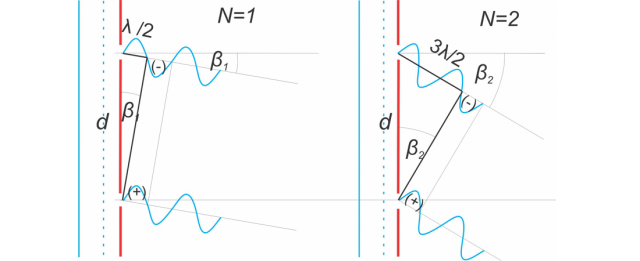
Figure 4: Attenuation: left image N = 1 (first-order minima), right image N = 2 (second-order minima)
A diffraction grating attenuates light of wavelength 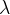in the direction 
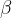if:
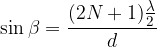
where:
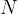is the order number, and
is the grating spacing.
So far, we have only observed light emanating from two adjacent slits. In reality, there are many slits, and at each, the light of a certain wavelength is diffracted at the same angle.
Let us imagine a diffraction grating with four slits as shown in Figure 6.
Figure 6: Diffraction grating
A beam of monochromatic (single wavelength) light incident perpendicularly on a grating is diffracted on it. We observe the direction where the rays are amplified. Let's denote it by . We see that this angle is the same for all rays emerging from the slits. The rays are parallel. The interference image they put on the screen is therefore as high as the diffraction grating is high or as wide as the beam of light.
In the case of multi-colored light, the interference images on the screen would overlap. We can help ourselves with a converging lens - Figure 7, which maps all parallel rays incident on the lens to a single point located in the focal plane. In this case, we get a point in the focal plane for each wavelength.
Figure 7: Diffraction grating with lens
