Personal collections


Let a force 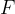 act on a flexible body (e.g. an elastic spring). Due to the action of the force, the body flexibly deforms: it stretches or contracts by
act on a flexible body (e.g. an elastic spring). Due to the action of the force, the body flexibly deforms: it stretches or contracts by 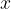 and thereby receives elastic energy.
and thereby receives elastic energy.
The characteristic of an elastic body is that it returns to its original shape when the force ceases to act. We say that the process is reversible. Elastic energy is converted back into mechanical work or into some other energy, for example, kinetic energy and (or) potential energy.
Elastic energy exists in, for example, a stretched bow with which we intend to shoot an arrow, a ball bouncing off the ground, an elastic rope during adrenaline-pumping jumps from a bridge, etc.
How do we get elastic energy?
In the chapter, Newton's Third Law of Motion, we learned about the formula that connects the force 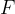 and the extension
and the extension 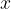 when an elastic spring is stretched (Hooke's law) which is given as:
when an elastic spring is stretched (Hooke's law) which is given as:

where 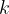 is a constant representing the hardness/stiffness of the spring.
is a constant representing the hardness/stiffness of the spring.
Let's draw a graph of the spring extension 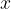 and the force
and the force 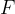 acting on the spring.
acting on the spring.
The force is not constant, it increases with extension 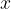 . At the final extension
. At the final extension 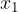 , the force is
, the force is 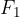 . When calculating the work of the force, we can take the product of the average force
. When calculating the work of the force, we can take the product of the average force 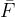 together with the distance covered which is equal to the final extension
together with the distance covered which is equal to the final extension 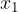 :
:
The expression on the right-hand side of the above equation is the elastic energy 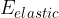 :
:
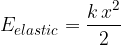
If a body deforms elastically due to the work of a force, it gains elastic energy which is given as:
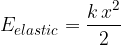
where 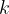 is the force constant of the spring and
is the force constant of the spring and 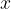 is the extension.
is the extension.
Let's extend the validity of the work-energy theorem: the work 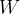 of a force is equal to the change in kinetic energy
of a force is equal to the change in kinetic energy 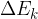 , potential energy
, potential energy 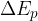 , and elastic energy
, and elastic energy 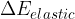 :
:
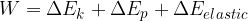
or:
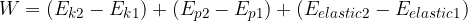
If no external force is acting, the total energy is conserved - energies are just converted from one form to another (law of conservation of energy):
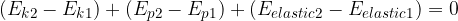
The work of a force is equal to the change in kinetic, potential, and elastic energy.
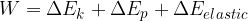
The law of conservation of energy says that if no external force acts on a body, the total energy is conserved - the energies are only converted from one form to another: