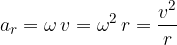Personal collections


In the material, Force as a vector, we learned that force can:
change the speed of motion of a body and/or
change the direction of motion of a body and/or
deform a body.
When a body rotates, it obviously changes its direction of motion. In this material, we will be interested in which forces cause this change and what happens during uniform circular motion.
In the material, Uniform circular motion, we mainly focused on the motion of the body, but we were not interested in its mass. But what if we consider that the body has mass?
If the body has mass and the motion is accelerated at the same time, we are dealing, in accordance with Newton's second law, with a force. The force is given by the formula:
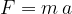
Since mass is not a vector and has no direction, the direction of the force is determined by the direction of the acceleration and as we found in the material, Uniform circular motion, the acceleration that causes a change in direction of motion is the radial acceleration 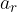 . The radial acceleration is perpendicular to the tangential velocity vector
. The radial acceleration is perpendicular to the tangential velocity vector 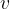 and points towards the centre of the circle (see Figure 2). The force called the radial force or centripetal force
and points towards the centre of the circle (see Figure 2). The force called the radial force or centripetal force 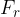 will also point in this direction.
will also point in this direction.
To clearly indicate that we are talking about radial force and radial acceleration, we equip the force formula with the index  :
:
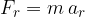
From the material, Uniform circular motion, we know that radial acceleration can be written in several different forms:
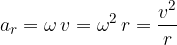
Each of the formulas of the radial acceleration 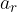 can be inserted into the formula of the radial force
can be inserted into the formula of the radial force 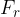 to get:
to get:
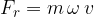
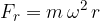
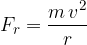
The causes of radial force can be very different. Here are a few:
The radial force can be provided by force frictional force between a body and the ground (an example is a car travelling around a corner in the introduction).
The rotation of a body on a string in a horizontal plane is enabled by a radial force equal to the force of the string on which the rotating body is suspended.
The orbit of the Moon around the Earth is made possible by the gravitational force between the Earth and the Moon.
The radial force can be the resultant of several forces (e.g., string force and gravitational force as seen in the example below).
A body of mass 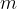 rotates due to the radial force
rotates due to the radial force 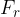 that forces it to rotate. If there are several forces affecting the rotation, the following applies: the resultant of all the forces acting on the rotating body is equal to the radial force. The radial force is calculated using the law of dynamics (Newton's second law):
that forces it to rotate. If there are several forces affecting the rotation, the following applies: the resultant of all the forces acting on the rotating body is equal to the radial force. The radial force is calculated using the law of dynamics (Newton's second law):
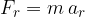
The radial acceleration 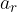 is calculated using one of the formulas below:
is calculated using one of the formulas below: