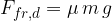Personal collections


In the figure below, a box rests on a flat surface. We apply force on the box to move it. We increase the force until it moves. With the force of our hands, before the box starts moving, we have to first overcome a resisting force called the static frictional force  (left image in Figure 1).
(left image in Figure 1).
When the box starts to move, we can slightly reduce the force of our hands (right image in Figure 1). We push the box so that it moves uniformly. According to the law of inertia, the sum of all forces acting on it will then be zero.
We conclude that since the body is moving uniformly, the sum of the forces on the body is zero. Therefore, in addition to our pulling force, another opposing force must act against the pulling force. It is called the dynamic frictional force  . This works in the opposite direction to the motion of the body.
. This works in the opposite direction to the motion of the body.
The static frictional force is a force that tends to prevent a body from moving. The dynamic frictional force is the force that impedes the movement of a moving body.
Let's now discuss both forces in detail.
A body of mass 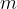 rests on level ground. It acts on the ground with its weight
rests on level ground. It acts on the ground with its weight 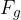 , which has a grip in the centre (centre of gravity) of the body and is directed vertically downwards and is given as:
, which has a grip in the centre (centre of gravity) of the body and is directed vertically downwards and is given as:
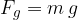
According to Newton's third law, an equally large ground force acts on the body, directed upwards and perpendicular to the ground. Since a perpendicular line is also called a normal, we label the ground force as a normal force 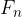 . It has a grip on the contact between the body and the ground. Therefore:
. It has a grip on the contact between the body and the ground. Therefore:
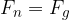
The surface between the body and the ground is rough (see Figure 2):
We first try to move the body with a small force (Figure 3, left). The body does not move; it looks as if it is glued to the surface due to its roughness.
Our small force is opposed by an equally large force, which we call the static frictional force  . It is directed in the opposite direction to the applied force
. It is directed in the opposite direction to the applied force  . Its grip is on the contact between the body and the surface. The sum of the applied force
. Its grip is on the contact between the body and the surface. The sum of the applied force  and the static frictional force
and the static frictional force  is zero and the body is at rest.
is zero and the body is at rest.
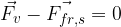
We gradually increase the applied or traction force  . In accordance with the mutual action of forces, the static frictional force
. In accordance with the mutual action of forces, the static frictional force  also increases. Suddenly, the body shifts and begins to move. Just before the start of the movement, the pulling force
also increases. Suddenly, the body shifts and begins to move. Just before the start of the movement, the pulling force 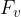 and the static frictional force
and the static frictional force  are the largest (Figure 3, right).
are the largest (Figure 3, right).
The static frictional force therefore increases from zero to a particular maximum value as the pulling force increases.
But how do we calculate the maximum static frictional force?
Experiments show that the static frictional force is:
independent of the area of the contact surface;
proportional to the ground or normal force. The proportionality constant depends on the type and roughness of the contact surface and is called the coefficient of static friction, 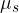 .
.
Let's obtain the expression for the static frictional force which is given as:
If a body is located on a flat surface, the maximum static frictional force  depends on the force
depends on the force 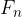 exerted by the surface on the body:
exerted by the surface on the body:
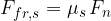
Therefore, for a body on a horizontal base:
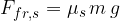
where 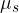 is the coefficient of the static friction which depends on the roughness of the contact surface between the body and the ground.
is the coefficient of the static friction which depends on the roughness of the contact surface between the body and the ground.
When we overcome the static frictional force and the body starts to move, the dynamic frictional force begins to act on the body (in addition to the traction force) instead of the force of adhesion  . The dynamic frictional force
. The dynamic frictional force  opposes the motion of the body.
opposes the motion of the body.
After we have overcome the static frictional force  , we act on the body with the traction of pulling force
, we act on the body with the traction of pulling force  . We want to pull the body uniformly and in a straight line, which happens when the pulling force is exactly equal in magnitude and opposite in direction to the dynamic frictional force. We find that we therefore need to reduce the pulling force so that it is slightly less than the force that was needed to overcome the static frictional force (Figure 4, left). From this, we conclude that the dynamic frictional force is a little less than the static frictional force.
. We want to pull the body uniformly and in a straight line, which happens when the pulling force is exactly equal in magnitude and opposite in direction to the dynamic frictional force. We find that we therefore need to reduce the pulling force so that it is slightly less than the force that was needed to overcome the static frictional force (Figure 4, left). From this, we conclude that the dynamic frictional force is a little less than the static frictional force.
Since the body moves uniformly and in a straight line, according to the law of law of inertia, the sum of all forces acting on it is zero. There is a pulling force  and the dynamic frictional force
and the dynamic frictional force  acting on the body. Therefore:
acting on the body. Therefore:
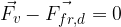
If we increase the traction force  , the dynamic frictional force
, the dynamic frictional force  will still remain the same. Their difference therefore will no longer be zero and the body will move with uniform acceleration in accordance with the law of dynamics:
will still remain the same. Their difference therefore will no longer be zero and the body will move with uniform acceleration in accordance with the law of dynamics:
If the traction force  falls below the frictional force, the body will stop.
falls below the frictional force, the body will stop.
The dynamic frictional force  is calculated similarly to the static frictional force
is calculated similarly to the static frictional force  . Instead of the static friction coefficient
. Instead of the static friction coefficient 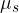 , we have the dynamic friction coefficient
, we have the dynamic friction coefficient 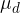 :
:
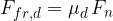
or:
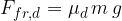
During the motion of the body, we have to overcome the dynamic frictional force  . It is given as the product of the coefficient o dynamic friction
. It is given as the product of the coefficient o dynamic friction 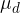 and the normal force
and the normal force 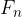 :
:
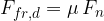
Therefore, for a body on a horizontal base: