Personal collections
The kinetic theory of gases is based on some simplifying assumptions. The molecules of the gas are assumed to behave as hard elastic identical spheres. State the assumption about ideal gas molecules based on
the nature of their movement,
their volume.
A cube of volume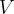 
contains 
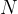molecules of an ideal gas. Each molecule has a component 
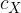of velocity normal to one side S of the cube, as shown in the figure below.
The pressure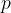 
of the gas due to the component 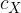of velocity is given by the expression
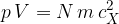
where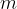 
is the mass of a molecule.
Explain how the expression leads to the relation
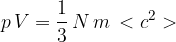
where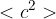 
is the mean square speed of the molecules.
The molecules of an ideal gas have a root-mean-square (r.m.s.) speed of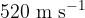 
at a temperature of 
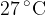. Calculate the r.m.s. speed of the molecules at a temperature of 
.
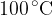