A magnet produces a uniform magnetic field of flux density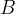 
in the space between its poles. A rigid copper wire carrying a current is balanced on a pivot. Part PQLM of the wire is between the poles of the magnet, as illustrated in the figure below.
The wire is balanced horizontally by means of a small weight W. The section of the wire between the poles of the magnet is shown in the figure below.
Explain why
section QL of the wire gives rise to a moment about the pivot,
sections PQ and LM of the wire do not affect the equilibrium of the wire.
Section QL of the wire has length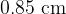 
. The perpendicular distance of QL from the pivot is 
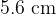. When the current in the wire is changed by 
, W is moved a distance of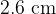 
along the wire in order to restore equilibrium. The mass of W is 
.
Show that the change in moment of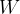 
about the pivot is 
.
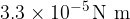Use the information in (i) to determine the magnetic flux density 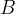between the poles of the magnet.
.
