The current in a long, straight vertical wire is in the direction XY, as shown in the figure below.
The current-carrying wire is within the Earth’s magnetic field. As a result, the pattern of the magnetic flux in the horizontal plane ABCD due to the current-carrying wire is superposed with the horizontal component of the Earth’s magnetic field. The figure below shows a plan view of the plane ABCD with the current in the wire coming out of the plane.
The horizontal component of the Earth’s magnetic field is also shown.
On the plan view above, mark with the letter P, a point where the magnetic field due to the current-carrying wire could be equal and opposite to that of the Earth.
For a long, straight wire carrying current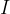 
, the magnetic flux density 
at distance 
from the centre of the wire is given by the expression
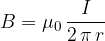
where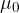 
is the permeability of free space. The point P in (i) is found to be 
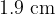from the centre of the wire for a current of 
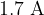. Calculate a value for the horizontal component of the Earth’s magnetic flux density.
The current in the wire in (a)(ii) is increased. The point P is now found to be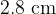 
from the wire. Determine the new current in the wire.
.
.
