Personal collections


A body moves if its position changes with time relative to another body or to a group of bodies in its surroundings. The surroundings are stationary and if we attach a coordinate system to it in our mind, we can describe the motion in this system. We say that motion is relative. The description of motion depends on the coordinate system in which the motion is described. Motion is different when viewed from a different coordinate system.
When describing motion, we always specify the coordinate system (surroundings) to which the motion refers. We attach the coordinate system to the surroundings and use it to measure the distance between the body and the selected starting point and measure the time with the clock. We usually choose a rectangular coordinate system in which the position of the body is described with x, y, and z-coordinates. The composition of a coordinate system and a clock is also called a coordinate system.

Figure 1: Airplanes move relative to the Earth, and the pilots in the airplanes see that the speed of one airplane relative to the other is zero
The airplanes flying shown in Figure 1 are moving at the same speed relative to the Earth. Pilots in the airplanes, on the other hand, see that the speed of the airplanes relative to each other is zero. We ourselves are currently moving at a speed of about 100,000 km/h, despite the fact that we are at rest relative to the Earth. Together with the Earth, we move around the Sun (revolution) and with the entire solar system in outer space.
How do we describe figures 2a and 2b, which show boats at two different moments? Is it possible to tell which of the two boats has moved in the time interval between the two shots, or is it possible that both have moved? Since we can't see the background, we can't answer the question with certainty.

Figures 2a, 2b: When observing the boats in two consecutive moments, it is difficult to determine which of the two has moved
However, when we see another part of the coast, as shown in Figures 3a and 3b, we find that only one boat has moved relative to the coast, and the other is stationary. The above examples show us that motion is relative and not absolute: a body moves at the same time with respect to a body that is at rest or moves at a different speed with respect to another moving body.

Figures 3a, 3b: If we add the background - the coast - to the images, we can determine which of the two boats has moved
In general, we can say that a body is moving if its position relative to another body or an observation system changes over time. When we describe the motion of a body, we must have an observer with a meter and a clock who can measure distances and time in an observation system that consists of one or more bodies whose positions change over time.
To explain the importance of choosing an observation system to describe the motion of an observed body, let's look at two buses moving towards each other on a straight road (Figures 4a, 4b, 4c). The speedometers on the buses show 80 km/h. We investigate the motion from three different observation points: one observation system is relative to the Earth, and the other two, are to the buses.
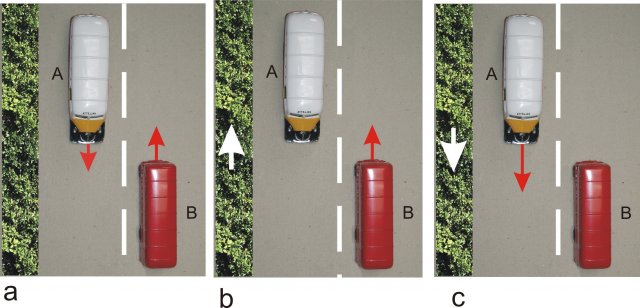
Figures 4a, 4b, 4c: The figures show two buses on a straight road with a hedge. Buses and hedges can be stationary or moving - depending on the choice of observation system
In the Earth-bound observation system, two buses are moving towards each other at a speed of 80 km/h, the hedgerow on the side of the road is stationary.
In the observation system, which is connected to bus A, bus B, and the hedge move in the same direction in the direction of the arrows at a speed of 160 km/h (bus B) or 80 km/h (hedge), and bus A is stationary.
In the observation system tied to bus B, bus A, and the hedge move in the same direction as shown by the arrows. with a speed of 160 km/h (bus A) or 80 km/h (hedge), and bus B is stationary.
The observation system in which the observed body is located will be tied to Earth. The axes of the coordinate system are perpendicular to each other. When describing motion, we limit ourselves to observing and describing the motion of one point of the body, regardless of the size of the moving body. The motion is generally spatial, the body moves in any direction. Depending on the path, the motion is divided into linear and curved. In linear motion, the body moves along a straight line, e.g. bus on a straight road while the motion of a skier on a slalom course is curved.
Depending on the path, motion is divided into linear and curved.
A body is anything that has shape and size. However, since we often focus on the laws of motion without being interested in other properties, we reduce the body in our mind to such a small size (point) that its size does not matter when describing the motion.
The observed body has the coordinates 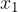 ,
, 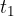 at one moment and
at one moment and  ,
, 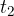 at the next moment.
at the next moment.
The distance 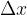 is the distance between the two positions
is the distance between the two positions 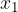 and
and 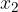 of the body in the time interval
of the body in the time interval 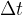 :
:
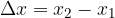
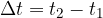
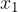 is the position of the body at the moment
is the position of the body at the moment 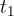 and
and 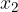 is the position of the body at the moment
is the position of the body at the moment 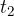 . The unit of measurement for distance is the metre (
. The unit of measurement for distance is the metre (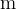 ).
).
When observing the motion of a body, we are often interested in the velocity  . Velocity tells us how fast the distance is changing with time. A body moves faster if it makes a greater distance
. Velocity tells us how fast the distance is changing with time. A body moves faster if it makes a greater distance 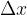 in a given time interval
in a given time interval 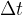 . In other words: the body moves faster if the body needs a shorter time interval
. In other words: the body moves faster if the body needs a shorter time interval 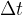 for a certain distance
for a certain distance 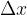 . The ratio of the distance
. The ratio of the distance 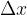 to that of the time interval
to that of the time interval 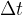 required for the distance is taken as a measure of velocity
required for the distance is taken as a measure of velocity  .
.

The unit of measurement of speed is metres per second (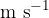 ).
).
Speed is also often given in 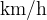 , so we have to change the unit to
, so we have to change the unit to 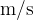 . The change is made according to the formula:
. The change is made according to the formula:
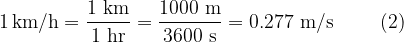
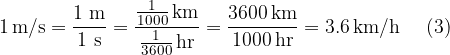
The speed calculated according to formula 1 is called the average speed. The average speed tells us how the body moves along the entire distance  in a time interval
in a time interval 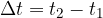 . If we want to know what happens with the speed within the distance in this time interval, we have to shorten the distance
. If we want to know what happens with the speed within the distance in this time interval, we have to shorten the distance 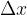 and the time interval
and the time interval 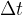 . In this way, we get the average speed in a shorter distance or in a shorter time interval. The intervals are shortened so that the results for the average speed at a given moment do not change, this speed is called the instantaneous speed
. In this way, we get the average speed in a shorter distance or in a shorter time interval. The intervals are shortened so that the results for the average speed at a given moment do not change, this speed is called the instantaneous speed  . The instantaneous speed is the average speed measured in a short time interval or on a short distance.
. The instantaneous speed is the average speed measured in a short time interval or on a short distance.
Depending on the speed, we divide motion into:
uniform motion, where the speed is always the same in magnitude and direction, and
non-uniform motion, where the velocity changes with time in magnitude and direction or by only one of the components.
We use graphs to describe the motions.

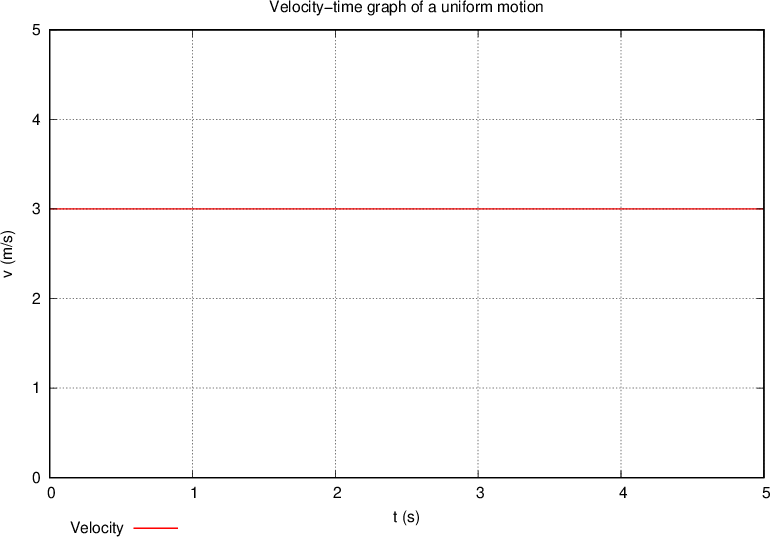
The graph shows the dependence of one physical quantity on another physical quantity.
The direction in which the body is moving is also important for describing motion. Velocity also has a direction, so it is a vector quantity.
A physical quantity that, in addition to magnitude, also has a direction is called a vector.