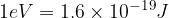An electrically charged particle can be stationary, moving uniformly or uniformly accelerated according to Newton's first and second laws which say that:
If the resultant of all forces acting on a particle is zero, the particle is at rest or moving uniformly and in a straight line.
If a constant force acts on a particle, it moves with uniform acceleration.
Let there be an electrically charged particle in an electric field. A constant electric force acts on it. Other forces such as gravitational force are ignored at this moment. Due to the action of the constant force, the particle will accelerate or decelerate uniformly.
If a constant electric force acts in the direction of the particle's motion, it moves uniformly accelerated. The acceleration is positive.
If an electric force acts in the opposite direction to the motion of the particle, its motion is uniformly decelerated. Acceleration is negative.
A moving electrically charged particle also has its own mass. A moving mass has kinetic energy. The unit for energy is the Joule [J]. In elementary particle physics, we often use a smaller unit - the electron volt [eV]. We will learn what this unit means later.
Let's place an electrically charged particle in an electric field. A force directed along the lines of force of the electric field begins to act on it. If the charge is positive, the force acts in the direction of the electric field lines, and if it is negative, it acts in the opposite direction. The magnitude of the electric force is:
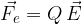
According to Newton's second law, the particle will begin to move uniformly accelerated with acceleration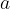 
:
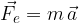
If we equate the right sides of both equations above, we have:
An electric force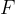 
acts on an electrically charged particle of charge quantity 
in an electric field of strength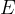 
. The force causes the particle to move uniformly with an acceleration 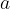given as:
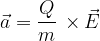
If we know the acceleration of an electrically charged particle, we can also calculate its speed after a certain time of motion and the distance it has travelled. Here, we use the knowledge and formulas we learned in the materials Uniformly Accelerated Motion for A-Level and Horizontal Projectile Motion.
Let's look at all possible movements by dividing them into:
motion that takes place only on a straight line (linear motion),
motion that takes place on a plane (planar motion).
The following examples of (linear) motion are possible. All motions are uniformly accelerated motions.
The particle is at rest at time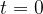 
, after which it starts to move with acceleration .
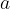Its speed 
is increasing and at time 
:
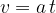
The distance 
travelled in time is:
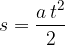
At time 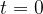, the particle has an initial velocity 
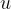. Then its speed increases with the acceleration .
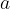Its initial speed continues to increase and at time , its speed is:
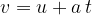
The distance travelled in time is:
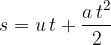
At time 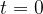, the particle has an initial velocity 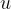, after which its velocity decreases with a deceleration .
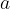Its speed at time is:
The distance travelled in time is:
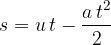
In planar motion, let's consider when the particle moves:
uniformly along the x-axis at spee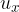d 
, and
when an electric force starts to act on it at time 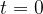, which causes the particle to move in the y-direction with an acceleration .
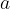It is calculated similarly to horizontal projectile motion.
Calculation of the velocity
At time , the x-component of the particle's velocity remains the same, since the motion in this direction is uniform:
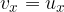
The y-component of the velocity increases with the acceleration :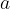
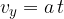
The total velocity is the vector sum of both components.
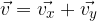
Its absolute value is calculated according to the Pythagorean theorem, rather than using angular functions:
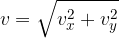
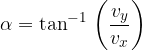
Calculation of the distance
In time , the particle covers a distance 
in the x-direction which is given as:
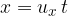
In the y-direction however, it covers the distance:
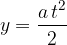
An electric force acts on an electrically charged particle over the distance . The work of the electric force is calculated using the equation:
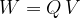
According to the kinetic energy theorem, the work done causes a change in the kinetic energy. Therefore:
The work of the electric force on an electrically charged particle is equal to the change in its kinetic energy:
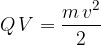
One electron volt is the energy gained by an electron (with a base charge of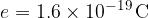 
) when it crosses a potential difference of 
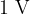unhindered:
