Personal collections


A mirror is a smooth surface (e.g. splined aluminum, silver, etc.) that reflects most of the incident light. Here, the law of reflection applies: the angle of incidence is equal to the angle of reflection.
The image of an object obtained by mirroring can be real or virtual. In the sketches, we will therefore mark the rays that give a real image with a solid line and the imaginary rays with a broken line. We will learn what is a real and what is a virtual image of an object using concrete examples.
We use a flat, concave, or convex mirror for imaging.
Most often we use a plane mirror. If we look at ourselves in a plane mirror, our mirror image is virtual (Figure 1). Real rays emanate from a single point of the body and are reflected on the mirror according to the law of reflection, but we see rays emanating from the virtual image of the object - we mark them with dashed lines. It seems to us as if our image is behind the mirror.
As an interesting point, we can mention that the condition to see ourselves in the mirror as a whole is that the height of the mirror is equal to half the height of the person and that the mirror is placed in such a way that the upper edge is at the height of the top of his head (red colored rectangle - "mirror" in Figure 1). The real ray emanating from the foot (lowest point) is reflected from the mirror precisely at the point where the mirror begins; in this case, the foot - the point of reflection - the eyes form an isosceles triangle (see Figure 1).
What is a concave mirror?
It is often difficult to remember whether a mirror is concave or convex. One of the tricks to connect a concave mirror with concavity is to pour coffee into the mirror.
A beam of light entering a concave mirror is collected after reflection and converges to a single point called the focal point or principal focus. It can also be the other way round - a point lamp, which is placed in the focal point so that after reflection a beam of parallel rays is produced (for example - a car reflector).
Let us now look at some terms and expressions that are used for all mirrors (not only concave) and are indicated in Figure 2.
Basic terms when dealing with mirrors:
The pole P is the centre of the mirror.
The principal axis is a line that passes through the centre of the mirror and is perpendicular to the surface of the mirror at point P.
The principal focus F is the point where rays that are parallel to the principal axis before reflection converge after reflection.
The focal length f is the distance between the principal focus and the pole of the mirror.
We often use a concave mirror to form the image of an object. An object of height 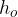 is placed at a distance
is placed at a distance 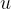 in front of the mirror. At a distance
in front of the mirror. At a distance 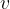 from the mirror, an image of height
from the mirror, an image of height 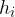 is obtained. The image can be diminished, the same size as the object, or enlarged depending on the position of the object. It can be upright or inverted. If real rays create the image, the image is real (Figure 3), but if virtual rays intersect (example in Figure 6), the image is virtual.
is obtained. The image can be diminished, the same size as the object, or enlarged depending on the position of the object. It can be upright or inverted. If real rays create the image, the image is real (Figure 3), but if virtual rays intersect (example in Figure 6), the image is virtual.
Regardless of where the object is and what the image is, we draw certain rays emanating from the object and watch how the rays are reflected on the mirror.
Names of the rays in the mirror:
An axial ray is a ray that is incident in the direction of the principal axis and does not change direction after reflection, i.e. it travels back along the principal axis. When drawing the image formation, the base of the object O and the image I are placed on the axis and mirrored as an axial ray.
A parietal ray is a ray that strikes the mirror's pole at a certain angle and is reflected from the pole at the same angle in the opposite direction.
A parallel ray is a ray that is parallel to the principal axis before reflection and passes through the principal focus after reflection.
A focal ray is a ray that passes through the principal focus before reflection and travels parallel to the oprincipal axis after reflection.
Looking at Figure 3, the image I of object O is real (intersecting real rays), diminished and inverted.
Rays that are parallel to the principal axis intersect at the point F called the principal focus. The point is located on the principal axis. The distance between the pole P and the principal focus F is called the focal length f. Point C in Figure 4 is the centre of curvature of the sphere of which the mirror forms a part.
The focal length of the mirror (spherical cap) is approximately equal to half the length of the radius of the sphere. Let's prove this claim!
Let us observe a parallel ray that is reflected from the mirror at point T. The radius  in Figure 4 represents the perpendicular to the surface where the ray is reflected. The law of reflection applies: the angle of incidence
in Figure 4 represents the perpendicular to the surface where the ray is reflected. The law of reflection applies: the angle of incidence 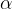 is equal to the angle of reflection. The angle between the radius (the distance between the points T and C) and the principal axis is equal to the angle of incidence
is equal to the angle of reflection. The angle between the radius (the distance between the points T and C) and the principal axis is equal to the angle of incidence 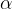 since these are alternating angles. It follows that the triangle TFC is an isosceles triangle with a base of length
since these are alternating angles. It follows that the triangle TFC is an isosceles triangle with a base of length  . The height of the triangle divides the base into two equal halves, i.e. at
. The height of the triangle divides the base into two equal halves, i.e. at 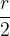 .
.
From Figure 4, we have:
We can see that in the case of a spherical cap, the principal focus depends on the angle of incidence 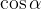 . Only at very small angles (small distances of the rays from the optical axis) can we consider the principal focus to be a point. In most cases, in practice, a parabola is used instead of a spherical cap, where the principal focus does not depend on the distance of the ray from the principal axis, or on the width of the light ray.
. Only at very small angles (small distances of the rays from the optical axis) can we consider the principal focus to be a point. In most cases, in practice, a parabola is used instead of a spherical cap, where the principal focus does not depend on the distance of the ray from the principal axis, or on the width of the light ray.
Only at very small angles (small distances of the rays from the principal axis) can we consider the principal focus of the mirror (spherical cap) to be a point.
The focal length of a spherical cap mirror is equal to half the radius of the sphere:
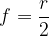
The equation is only valid if the rays are incident on the mirror near the principal axis. Because of this limitation, parabolas are usually used in practice. With a parabola, all rays that are parallel to the principal axis converge at the principal focus.
The mirror equations relate the heights of the image and object, their distances from the mirror, and the focal length. The equations of a concave mirror (which also apply to a convex mirror and lenses) are obtained by observing the similar triangles in Figure 5:
First, let's look at the orange-hatched triangles. We see that the height of the image relative to that of the object is in the same ratio as their distances from the vertex of the mirror:

where 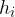 is the height of the image, and
is the height of the image, and 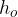 is the height of the object.
is the height of the object.
Now, let's observe the similar triangles hatched with oblique lines. We have:
The mirror formulas are:
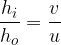
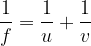
where 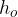 is the height of the object,
is the height of the object, 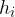 is the height of the image,
is the height of the image, 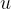 is the distance of the object from the mirror,
is the distance of the object from the mirror, 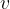 is the distance of the image from the mirror, and
is the distance of the image from the mirror, and 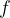 is the focal length.
is the focal length.
In an inverted image, we took a positive 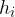 ; if the image is upright,
; if the image is upright, 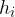 will therefore be negative.
will therefore be negative.
The distance 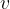 and focal length
and focal length 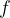 can be positive or negative. The negative distance is always the distance of a virtual image formed by the apparent intersection of rays (see the example in Figure 6) or the apparent focal length, which will be illustrated in the case of a scattering mirror (Figure 7).
can be positive or negative. The negative distance is always the distance of a virtual image formed by the apparent intersection of rays (see the example in Figure 6) or the apparent focal length, which will be illustrated in the case of a scattering mirror (Figure 7).
A convex mirror consists of a convex spherical cap or a parabola. In the case of a convex or diverging mirror, the rays falling on it are diverged after reflection. They will never intersect on the object side. However, the virtual rays intersect, which are shown as an extension of the real reflected rays - Figure 6. We mark them with a broken line. The image is therefore virtual. From Figure 6 we can also see that the image of the object is upright and diminished.
The mirror equations that we derived for a concave mirror still apply, but we must take into account that the focal length 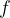 is negative in the data. The mirror radius
is negative in the data. The mirror radius  will also be negative. As a result of the calculation (see example), we will see that image distance
will also be negative. As a result of the calculation (see example), we will see that image distance 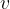 and height
and height 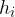 will also be negative.
will also be negative.
The image is located behind the mirror somewhere between the pole and the principal focus. The distance of the image from the mirror is always smaller than the distance of the object from the mirror. The higher the radius or focal length of the mirror, the more the absolute values of the distances are equal:
For proof, we write the mirror equation where take into account that 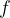 is negative:
is negative:
It is also true that when the object is at a large distance from the mirror, its apparent image goes towards the principal focus.
Proof:
The image of a convex mirror is always virtual since real rays diverge on the side of the object. The image is upright, and the focal length and the distance of the image from the mirror are negative.
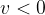
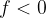
The absolute value of the distance 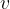 of the image from the mirror is always smaller than the distance
of the image from the mirror is always smaller than the distance 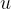 of the object:
of the object:
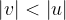
It follows that the height of the image is always smaller than the height of the object since the formula below says:
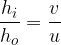
The virtual image moves towards the principal focus as the object distance moves towards infinity.