Personal collections


An electric oscillating circuit is an electric circuit that serves to generate high-frequency alternating voltage. It is basically an "electric" pendulum consisting of a parallel connection of a capacitor and an inductor (coil).
It is characteristic of an electric oscillating circuit that the energy of the electric field of the capacitor periodically flows into the energy of the magnetic field of the inductor (coil) and vice versa. If we posit an analogy with a mechanical simple pendulum, the charged capacitor represents potential energy and the inductor represents kinetic energy.
Let us assume that the oscillation of the oscillating circuit is harmonic and that the voltage 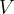 across the capacitor (and inductor, since they are connected in parallel) varies according to cosine:
across the capacitor (and inductor, since they are connected in parallel) varies according to cosine:

As the voltage changes over time, the charge 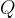 on the capacitor also changes:
on the capacitor also changes:
We obtained a current function whose maximum value is:

Let's summarize.
Assuming that:
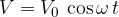
we obtained
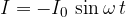
where
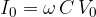
This chapter is intended for students who have already mastered the chapter, Derivatives. Students with no knowledge of derivatives can safely skip this part - while still following the explanation below.
We want to derive:
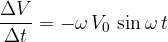
however, we know that:
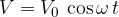
The symbol 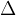 is often used as a high school substitute for
is often used as a high school substitute for 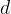 in calculus.
in calculus. 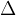 means a difference (e.g. a time difference), and this difference can be arbitrarily large. The symbol
means a difference (e.g. a time difference), and this difference can be arbitrarily large. The symbol 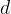 , like
, like 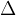 , also means a difference, but only an infinitesimal difference.
, also means a difference, but only an infinitesimal difference.
The equation:
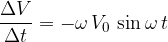
is actually just a high school approximation; the correct equation is:

or rather, we are looking for the derivative of voltage with respect to time. From the theory of derivatives, we know that:
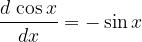
and therefore:
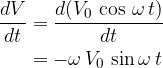
Due to the changing current as shown by equation 2, a voltage 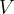 is induced in the inductor (coil) which is given as:
is induced in the inductor (coil) which is given as:
Again, we obtained the cosine form of the voltage, which is also present in the capacitor - equation (1). This is understandable since the induced voltage in the coil is equal to the voltage in the capacitor at every moment (the two elements are connected in parallel).
This chapter is intended for students who have already mastered the chapter, Derivatives. Students with no knowledge of derivatives can safely skip this part - while still following the explanation below.
We want to derive:
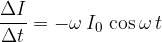
where the current 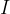 is given, as derived in equation 2, as:
is given, as derived in equation 2, as:
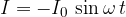
The symbol 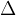 is often used as a high school substitute for
is often used as a high school substitute for 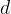 in calculus.
in calculus. 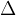 means a difference (e.g. a time difference), and this difference can be arbitrarily large. The symbol
means a difference (e.g. a time difference), and this difference can be arbitrarily large. The symbol 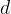 , like
, like 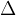 , also means a difference, but only an infinitesimal difference.
, also means a difference, but only an infinitesimal difference.
The equation:
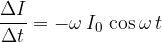
is actually just a high school approximation, the real equation is:

or rather, we are looking for the derivative of current with respect to time. From the theory of derivatives, we know that:
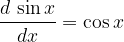
and therefore:

If we excite an oscillating circuit, e.g. by charging the capacitor with the help of an external voltage, the circuit oscillates with its own frequency.
In order to calculate the natural oscillation frequency 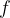 , we equate the voltage across the capacitor (equation 1) and the voltage across the inductor (equation 4):
, we equate the voltage across the capacitor (equation 1) and the voltage across the inductor (equation 4):
We have obtained an expression for the frequency of the oscillating circuit. At the same time, we showed that the oscillation is indeed harmonic because otherwise, we would not be able to equate the voltages across the inductor and the capacitor.
The natural or resonant frequency 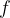 of an oscillating circuit is given as:
of an oscillating circuit is given as:
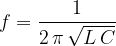
During the oscillation of an oscillating circuit, the energy is converted from the energy of the electric field of the capacitor into the energy of the magnetic field of the inductor in such a way that the sum of the two energies is constant at every moment.
Let's assume that at the first moment, all the energy is in the capacitor because at that time there is a maximum voltage across it (see the figure Graph of the voltage and current function of the oscillating circuit).
The electrical energy 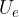 of the capacitor is equal to the work
of the capacitor is equal to the work 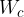 required to charge the capacitor (see also the chapter, Capacitor) to the voltage
required to charge the capacitor (see also the chapter, Capacitor) to the voltage 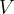 . It is equal to the area under the graph of the function, which shows the relationship between the charge
. It is equal to the area under the graph of the function, which shows the relationship between the charge 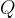 on the capacitor and the voltage
on the capacitor and the voltage 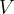 .
.
If we look at the graph of the voltage and current function, we see that the voltage across the capacitor is zero for a quarter of the period from the beginning of the observation. The capacitor then has no energy, all the energy is in the energy of the magnetic field of the coil, through which the maximum current now flows.
According to Lenz's rule, the inductor resists changes in current due to the voltage 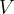 of its own induction. For the current to flow through the inductor, we need work
of its own induction. For the current to flow through the inductor, we need work 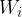 , which is equal to the area under the voltage graph V(Q):
, which is equal to the area under the voltage graph V(Q):
At any moment, the sum of electric and magnetic energy is constant and equal to the maximum energy of the electric or magnetic field:

Let's once again check the validity of the equation for the natural frequency. For this purpose, we equate the maximum value of electric and magnetic energy:
Through energy, we arrived at the same expression for the natural frequency of the oscillating circle as in the original calculation.
Let's summarize:
The electric energy 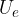 of the capacitor:
of the capacitor:
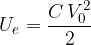
is harmoniously transformed into the magnetic energy 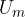 of the inductor in the electric oscillating circuit which is given as:
of the inductor in the electric oscillating circuit which is given as:
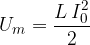
The sum of the two energies is constant at any moment and is equal to the maximum energy of the inductor or capacitor.
The energy oscillates at twice the frequency of the voltage.