Potential energy is a type of energy that a body has due to height.
Water in high-storage lakes has potential energy. In the event of a lack of other energy sources, it can be used to e.g. during the discharge of the accumulation, drive the turbines with an electric generator - in this case, the potential energy is converted into electricity. An avalanche on the hills can also have potential energy, which can do destructive work on its way to the valley.
Figure 1: Potential energy can be positive, negative, or zero.
The concept of body height in terms of potential energy has no absolute meaning, as, for example, absolute height is equal to the height of the object relative to sea level. We almost always mean relative height with respect to some other chosen reference height (ground, soil, valley, table top, etc.) where we say that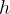 
is equal to zero. Depending on the chosen height, the potential energy can be positive (the body is above the chosen height), equal to zero (the body is at the chosen height), or negative (the body is below the chosen height).
The notation for potential energy is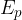 
, and the unit is Joule (
).
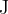A body has potential energy due to height.
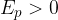if the height 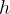is greater than the selected reference height.
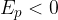if the height 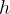is less than the selected reference height.
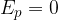if the body is at the selected reference height.
How do we obtain potential energy?
In the chapter, Kinetic energy, we learned about the work-energy theorem. This says that the kinetic energy of a body changes under the influence of the work of a force. This change could be an increase or a decrease:
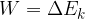
At that time, we tacitly assumed that the body was moving horizontally. What if it moves vertically?
The work-energy theorem still holds and the equation for the work of force also still applies:
The force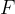 
is now the force of gravity (weight) 
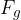, and the distance 
is the height difference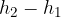 
:
In the formula below, the expression on the right-hand side is called potential energy:
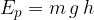
We emphasize: the term potential energy is used instead of the work of gravity. Therefore, in the calculations, we no longer take into account the work of the force of gravity but replace it with potential energy.
If the object does not move vertically, only the vertical component of the distance is taken into consideration - i.e. the height difference (see Figure 2).
Figure 2: Car on a hill
The potential energy is equal to the work of the force of gravity along the distance equal to the height .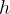
In the energy formulas, we only use potential energy, since the work of the force of gravity is already covered in potential energy:
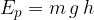
If the body moves down a slope, we take 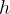as the vertical component of the distance.
Let's extend the validity of the work-energy theorem: the work of a force is equal to the change in kinetic and potential energy. It means the work of external forces acting on a body. The force of gravity is excluded, as it is already taken into account in the potential energy:
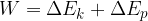
or:
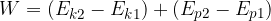
The application of the theorem will be best understood with an example:
The work of a force on a body is equal to the change in kinetic and potential energy of the body:
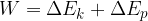
The change in kinetic energy is the final kinetic energy minus the initial kinetic energy:
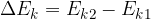
The change in potential energy is the final potential energy minus the initial potential energy:
The principle of conservation of energy states that:
If there is no work by an external force, energy is conserved:
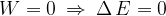
The law applies generally to all types of energy. For now, we will only use it for kinetic and potential energy:
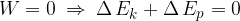
We can also learn from the above example that sometimes in physics, we arrive at the same results in different ways. The formula for the velocity during free fall (equation 1 above) was already learned in the chapter, Vertical motion under gravity.
