Personal collections


In the chapter, Density of a substance, we learned that the same substance can appear in three states:
solid
liquid
gaseous
The substances in the liquid or gaseous state are called fluids.
Pressure also acts inside fluids. The equation we learned in the chapter, Deformation of solids still holds:
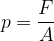
The problem is that at the first moment, we do not know what the force is in our case and what the surface area on which the force acts. To clear up the dilemma, let's first look at the mechanism of pressure in fluids. It can be interpreted in two ways:
Pressure caused by moving molecules
Pressure in fluids can be explained by observing the motion of molecules of substances in a closed container. Molecules move at a high speed, which depends on the mass of the molecules and on the temperature. Since they move in all directions, the motion on average cancels each other out and therefore the motion of the fluid as a whole is not detected. In this way, the moving molecules collide with the wall of the container and thereby create pressure. More precisely, the pressure of the force on the walls of the container is explained in the chapter, Gas laws and ideal gas equation.
The pressure of the fluid's gravity
A stationary liquid can also be viewed as a substance that has its own weight. When the force of gravity acts on the surface area 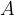 , it creates a pressure
, it creates a pressure  . How we calculate it will be explained a little below.
. How we calculate it will be explained a little below.
It is interesting that the pressure in fluids does not only act vertically downwards (as we are used to the force of gravity (weight) acting), but the force acts in all directions (Figure 1).
Let's calculate how much pressure acts on the horizontal plane of the surface area  , which is located at a depth
, which is located at a depth 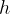 of the fluid with a density
of the fluid with a density 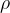 as shown in Figure 2. Let's assume that the density of the fluid does not change with depth.
as shown in Figure 2. Let's assume that the density of the fluid does not change with depth.
The surface area 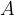 is acted upon by the weight
is acted upon by the weight 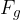 of the fluid, which is above the surface area
of the fluid, which is above the surface area 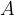 and creates a pressure
and creates a pressure 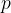 :
:
The pressure in the fluid does not depend on the surface area 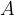 , but only on the depth
, but only on the depth 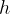 and the density
and the density 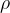 . It acts in all directions, not only downwards, which we already learned in the introductory chapter.
. It acts in all directions, not only downwards, which we already learned in the introductory chapter.
The pressure in a fluid depends only on the depth 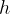 , the density
, the density 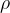 of the fluid and on the gravitational acceleration
of the fluid and on the gravitational acceleration 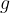 :
:

Air forms a mantle around the Earth. The equation for pressure, which we derived in the previous chapter, cannot be directly applied in the case of air. This is because air is compressible and the weight of air in higher layers affects its density in lower layers. Air density is also affected by the temperature, which is much lower at high altitudes than at ground level. The equation for pressure gets quite complicated:

In equation (2), air density no longer appears as a constant, but changes with altitude and temperature. Therefore, equation (2) can only be used approximately when it comes to smaller height differences and we can assume that the air density has not changed significantly with height and that the temperature in the observed area is also constant.
The air pressure on the Earth's surface is about 1 bar or 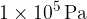 . It changes a little with the temperature, and altitude of the place and also depends on the weather.
. It changes a little with the temperature, and altitude of the place and also depends on the weather.
The air pressure on the Earth's surface is (on average):
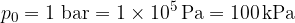
When calculating the liquid pressure at a depth  in an open container, we must also take into account the air pressure above the liquid. The air pressure and liquid pressure (e.g. water) are added together.
in an open container, we must also take into account the air pressure above the liquid. The air pressure and liquid pressure (e.g. water) are added together.
The insights we have gained are applied in many tools and measuring devices. Some are listed below:
First, let's draw a sketch of a connecting vessel:
Let's take the U-tube as shown in Figure 4 and pour water or some other liquid into one arm. The water will also fill the second arm so that the two levels will be equal. Since the arms are open at the top, air pressure  acts on the water in both arms of the tube. With depth, the pressure increases due to the weight of the water. At depth
acts on the water in both arms of the tube. With depth, the pressure increases due to the weight of the water. At depth 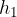 , the pressure is the same in both arms:
, the pressure is the same in both arms:
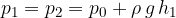
The maximum pressure is of course at the bottom of the connecting vessel:
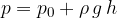
Let's pour two different liquids with different densities into the connecting vessel. We must make sure that the liquids do not mix. In this case, the liquid level is lower in the arm where the density is higher.
In the plane representing the boundary between the liquids (dashed line in Figure 5), the pressures on both arms are the same. Therefore:
To make it easier to imagine the operation of a siphon, let's draw it:
A siphon tube is a device with the help of which liquid can be passed, e.g. from a barrel to a lower container. It only works if we fill the tube with the liquid in some way in the beginning - e.g., we suck the liquid into the tube or fill the tube with the liquid before putting it in the container.
In order for the liquid to flow out of the barrel, two conditions must be met:
First condition for siphon to work
Everywhere in the tube, a positive pressure difference must be directed towards the outlet of the tube, otherwise, the liquid will not flow through the tube out of the barrel.
Let's observe the pressure 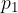 at the top of the siphon caused by the liquid in the left arm of the tube according to Figure 6. The pressure of the left arm at the level of the liquid surface in the barrel must be equal to the air pressure - that is:
at the top of the siphon caused by the liquid in the left arm of the tube according to Figure 6. The pressure of the left arm at the level of the liquid surface in the barrel must be equal to the air pressure - that is:
Similarly, the pressure  caused by the liquid in the right arm of the tube is:
caused by the liquid in the right arm of the tube is:

The pressure difference therefore will be:
If  , the difference is positive and the liquid will flow out of the barrel.
, the difference is positive and the liquid will flow out of the barrel.
Second condition for siphon to work
Another condition for the siphon to work is that the pressure 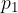 is positive. In other words: the pressure of the liquid at height
is positive. In other words: the pressure of the liquid at height 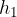 at the left arm of the tube must be less than the air pressure
at the left arm of the tube must be less than the air pressure 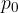 , which allows the liquid to rise up the left arm of the tube.
, which allows the liquid to rise up the left arm of the tube.
Let's draw a sketch of a hydraulic press:
A hydraulic press consists of a tube with a piston at each end - Figure 7. The tube is filled with a liquid - e.g. oil. The pistons have different surface areas 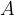 . A force
. A force 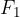 is applied to the piston with a smaller surface area
is applied to the piston with a smaller surface area 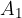 . To keep the system in balance, we also apply a force
. To keep the system in balance, we also apply a force 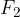 on the piston with a bigger surface area
on the piston with a bigger surface area 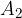 .
.
Similar to the connecting vessel, the pressure of the liquid depends on the external pressure - i.e. the pressure with which the piston presses on the liquid and on the depth where the pressure is observed. In our case, we observe the pressure only under the piston when the depth is zero. Since the pistons are approximately at the same height, there is no pressure difference due to fluid pressure, or it is much less than the pressure exerted by the two forces on the piston. Therefore, the following applies:
A gas pressure gauge, or manometer, compares the pressure of a gas with the pressure exerted by a column of a liquid in a tube. The tube is connected on one side to a container filled with gas at pressure 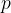 . The liquid in the tube rises by
. The liquid in the tube rises by 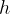 due to the pressure of the gas - see Figure 8. We calculate the gas pressure from the rise of the liquid using the formula:
due to the pressure of the gas - see Figure 8. We calculate the gas pressure from the rise of the liquid using the formula:
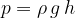
Air pressure does not affect the measurement, as the tube above the liquid is hermetically sealed and there is an airless space in it (no molecules - no pressure).
An air pressure gauge or barometer works similarly to a manometer. The coiled tube has a reservoir with the measuring liquid on one side. On the other side, the tube is sealed (and there is a vacuum in it). The air pressure acts on the measuring liquid only on the reservoir side, on the other side, the air pressure is balanced by the liquid pressure. The reservoir must have a sufficient volume so that the change in the height of the liquid on the measuring part of the tube is not significantly reflected in the height of the liquid in the reservoir.