Personal collections


We speak of a transverse wave when the particles move perpendicular to the direction of the wave motion. An example of a transverse wave is e.g. a wave on a long tensioned string that is swung on one side by hand. The wave propagates along the string while the string particles oscillate perpendicular to the string as shown in the figure below.
A sinusoidal transverse wave is obtained by exciting the beginning of a string according to a sine function of time. The wave that is created on the string at a certain moment of observation (let it be at the moment 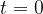 ) looks like the figure below:
) looks like the figure below:
The wave in Figure 2 is not stationary but travels along the x-axis with speed 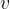 . If we were to observe only one particle of the string at some distance
. If we were to observe only one particle of the string at some distance 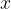 from the origin, we would see that this particle oscillates sinusoidally in the direction of the y-axis with a certain period
from the origin, we would see that this particle oscillates sinusoidally in the direction of the y-axis with a certain period 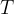 , frequency
, frequency 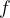 and amplitude
and amplitude 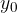 (the listed terms are described in the chapter, Simple harmonic motion).
(the listed terms are described in the chapter, Simple harmonic motion).
Before moving on to the mathematical notation of the equations, let's first write down the basic concepts of transverse waves. We will explain the listed terms in detail later.
A harmonic or sinusoidal transverse wave is a wave where particles oscillate perpendicular to the direction of wave propagation and their displacement 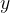 from the equilibrium position can be described as a sine function of distance and time.
from the equilibrium position can be described as a sine function of distance and time.
The amplitude 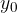 of a transverse wave is the maximum or peak displacement of the wave from the equilibrium position (from the x-axis in Figure 2). The maximum displacement is also called the crest (hill) of the wave and in the opposite direction the trough (valley) of the wave.
of a transverse wave is the maximum or peak displacement of the wave from the equilibrium position (from the x-axis in Figure 2). The maximum displacement is also called the crest (hill) of the wave and in the opposite direction the trough (valley) of the wave.
The period 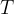 is the time when two crests or two troughs of the wave follow each other in the observed distance
is the time when two crests or two troughs of the wave follow each other in the observed distance 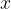 . (The term period has the same meaning as the time taken to complete a cycle or the oscillation period in an oscillation).
. (The term period has the same meaning as the time taken to complete a cycle or the oscillation period in an oscillation).
The Wavelength  is the length of one wave, for example, the distance between two crests or troughs of a wave.
is the length of one wave, for example, the distance between two crests or troughs of a wave.
The frequency 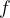 of a wave is the reciprocal of the period
of a wave is the reciprocal of the period 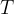 . It tells how many times per second the wave oscillates.
. It tells how many times per second the wave oscillates.
The speed of a wave is denoted by 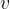 . A wave moves uniformly along the x-axis, i.e. in a direction perpendicular to the oscillation of the particles.
. A wave moves uniformly along the x-axis, i.e. in a direction perpendicular to the oscillation of the particles.
Let's excite the string in Figure 1 e.g., with a constant sinusoidal oscillation of the arm. The displacement of the string from the equilibrium position can therefore be described by the same equation as we learned in the chapter, Simple harmonic motion:

The oscillations caused at the beginning of the string propagate along the string with a uniform speed 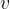 . The same equation applies to the distance
. The same equation applies to the distance  as in uniform motion:
as in uniform motion:

In this case, the distance of one wavelength  is equal to the product of:
is equal to the product of:
the wave propagation velocity 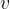 , and
, and
the period 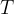 .
.
We write the equation:
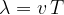
We note that the period 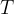 is the reciprocal of the frequency
is the reciprocal of the frequency 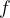 :
:

Therefore:

or:

The frequency 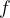 and wavelength
and wavelength  are inversely proportional. They are related by the formula:
are inversely proportional. They are related by the formula:
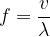
where 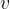 is the speed of the wave.
is the speed of the wave.
We have described the progressive transverse wave. The string oscillates transversely, and the wave propagates longitudinally along the string. The instantaneous displacement  of the string from its equilibrium position at a distance
of the string from its equilibrium position at a distance  from the origin of the string will depend on the time
from the origin of the string will depend on the time 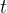 and the distance
and the distance 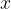 .
.
With the equation:
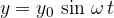
we can determine:
the displacement 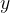 from the equilibrium position for any time at the starting position
from the equilibrium position for any time at the starting position 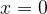 ,
,
or displacement 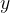 from the equilibrium position for any place in time
from the equilibrium position for any place in time  if we replace
if we replace 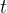 with
with  since
since 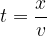 and get:
and get:
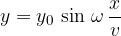
However, we would like an equation that could be used to determine the displacement from the equilibrium position:
at any time
for any place at the same time.
Thus, we derive the equation by first imagining a wave that has moved (see Figure 3). At time 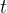 , the wave has moved by:
, the wave has moved by:
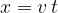
With our equation, let's try to track a point that is not far from the equilibrium position. Obviously, we can do this with the equation:
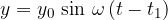
Let's check: if we insert  into the equation, the argument of the sine function is equal to 0 and the amplitude is also 0 - as it should be. The equation already allows us to choose any moment
into the equation, the argument of the sine function is equal to 0 and the amplitude is also 0 - as it should be. The equation already allows us to choose any moment 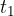 of the wave. But since we want to choose an arbitrary coordinate
of the wave. But since we want to choose an arbitrary coordinate 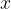 at the same time, we introduce the coordinate
at the same time, we introduce the coordinate 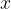 via time
via time 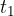 .
.
Let's derive the equation from the equation above:
The sine argument in the above equation shows the dependence of the displacement from the equilibrium on two terms:
the time 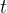 , and
, and
the distance 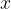 .
.
If we put 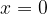 into the equation, we get the dependence on time (see Figure 4 left):
into the equation, we get the dependence on time (see Figure 4 left):
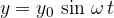
If we put 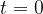 into the equation, we get the dependence on the distance (see Figure 4 right):
into the equation, we get the dependence on the distance (see Figure 4 right):

The equation for a progressive transverse wave is given as:
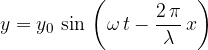
where 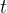 is any moment of the wave and
is any moment of the wave and 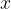 is also any coordinate of the wave.
is also any coordinate of the wave.
The wave speed on a stretched string or string is calculated according to the equation:

where 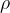 is the density of the string which is given as:
is the density of the string which is given as:

and 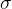 is the tensile stress which is given as:
is the tensile stress which is given as:

Let's therefore obtain the common form of the formula of the wave speed in a tensioned spring by inserting equations 5 and 6 into equation 4: