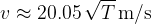Personal collections


In the material, Progressive longitudinal wave, we learned how a longitudinal wave is formed and how it propagates using the example of a helical spring.
In this material, we will apply the acquired knowledge to sound, since sound is also a longitudinal wave. Sound is produced by sound systems, i.e. vocal cords, musical instruments, speakers, etc. It spreads through the air, but it can also spread through liquid or solid matter. We will see that the smaller the compressibility of the substance through which it travels, the faster it spreads. A gas (e.g. air) is the most compressible, so the speed of sound in a gas is the lowest. Then comes liquid and solid matter, where the speed of sound is much higher.
When sound reaches our ears, we may or may not hear it. Humans only hear sound with frequencies (approximately) from 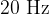 to
to 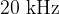 . Lower frequencies are called infrasound, and higher frequencies are called ultrasound, and we do not hear them.
. Lower frequencies are called infrasound, and higher frequencies are called ultrasound, and we do not hear them.
In this material we will learn:
how sound is made,
how sound is propagated, and
what its speed is.
The sound that we humans hear has frequencies from 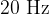 to
to 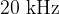 #. Lower frequencies are called infrasound, and higher frequencies are called ultrasound.
#. Lower frequencies are called infrasound, and higher frequencies are called ultrasound.
A sound source is always something that oscillates. By oscillating, it causes rarefactions and compressions to form in the medium (usually in the air) through which the sound travels. At the region of rarefaction, a vacuum of air is created, and at the region of compression, there is a concentration of air. Rarefaction and compression propagate away from the source as progressive longitudinal wave.
Let's discuss how sound is created, how it propagates, and how we receive it using the example below.
The oscillation of the diaphragm is also transmitted to molecules in the air near the diaphragm. This creates rarefactions and compressions that travel through the air away from the source. Let's imagine that at some point, we capture an image of the oscillation of the molecules and observe:
where the molecules are most concentrated and least concentrated,
where the pressure is maximum and minimum,
where the displacements of the molecules during oscillation are the highest and lowest.
The figure below shows a progressive longitudinal wave at time 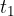 :
:
the upper image indicates the rarefactions and compressions along the wave,
the middle image is the graph of the change in pressure from position 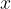 , and
, and
the lower image is a graph of the instantaneous (current) displacement of the air particles from the equilibrium position as a function of position 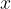 .
.
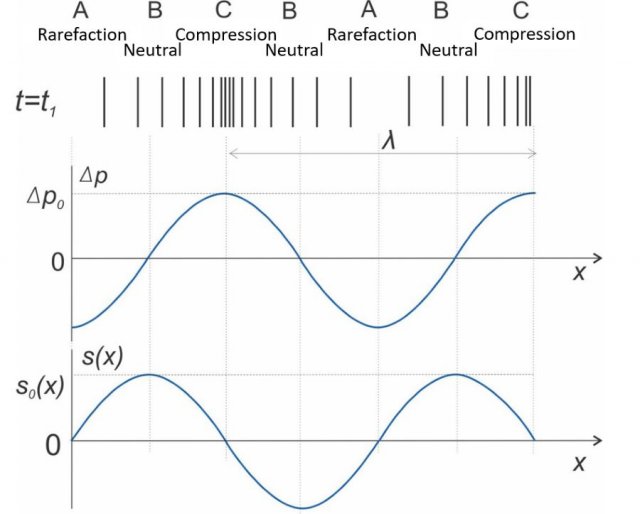
Figure3: Rarefactions, compressions, pressure changes 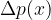 and displacement
and displacement  from the equilibrium during time
from the equilibrium during time 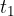
As we already learned in the material, Progressive longitudinal wave, the maximum displacement of air particles from the equilibrium position is in the position where the change in air pressure is equal to zero.
The points in Figure 3 are defined below:
A - air rarefaction. At the place where the rarefaction is currently, there is the least air pressure  . The current value of the displacement of air particles
. The current value of the displacement of air particles 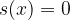 .
.
B - neutral position. Here, there is no change in pressure, but there is a maximum displacement 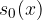 from the equilibrium position.
from the equilibrium position.
C - air compression. Here is the highest air pressure  , and the value of the current displacement
, and the value of the current displacement  is zero.
is zero.
Sound is a longitudinal wave of particles of matter, i.e. gas, liquid, or solid. Particles do not oscillate simultaneously throughout the entire medium, so compressions and rarefactions are formed along the medium. At the compression region, the pressure is increased, and at the rarefaction region, it is reduced. Compressions and rarefactions propagate through the medium as longitudinal waves.
The sound source can be any oscillator that causes longitudinal waves. Humans produce sound with vocal cords, with the help of musical instruments, or with the help of electronic devices.
The oscillation of the sound source can be a forced oscillation or a self-oscillation (e.g. a stretched string or air in a flute).
A sound source can emit sound with a single frequency. We call it tone. In addition to the tone of a certain frequency, musical instruments also emit multiples of these frequencies. We call this, a sound. More about this can be found in the material, Sound energy.
Musical instruments usually work based on the self-oscillation of a stretched material or air in a tube.
The following work on the basis of the self-oscillation of a stretched material:
self-oscillation of a string: This occurs in string instruments like violin, cello, guitar, and keyboard instruments like the piano.
self-oscillation of wooden or metal plates: This occurs in instruments like xylophones, vibraphones, etc.,
Self-oscillation of a stretched membrane: This occurs in the percussion (e.g. drums).
The following work on the basis of the self-oscillation of air in a pipe:
Wind instruments: flute, clarinet, saxophone, organ, etc.,
Brass instruments: horn, trumpet, trombone.
To tune musical instruments, we use tuning forks - figure 6. They are most often tuned to a musical tone with a frequency of  .
.
A tuning fork oscillates harmonically, i.e. produces a sine wave tone. We place them next to a musical instrument, e.g. piano so that the surface of the piano amplifies the sound, and we compare the tone frequency of the tuning fork and that of the instrument.
We can also use electronic synthesizers to help shape the sound. Electronic sound synthesizers enhance sound with the help of electronic circuits. They equip the base tone with higher harmonic components of the base tone. They produce sound of various musical instruments, add rhythm, accompaniment, and special sound effects - e.g. artificial echo.
A longitudinal wave in space can be imagined with the help of wave rays and wavefronts (see the figure below):
A wave ray is an imaginary line that indicates the direction in which the wave is propagating.
A wavefront is a surface that connects all places in space where the same density is currently located. The distance between two wavefronts is equal to the wavelength. The wavefront is perpendicular to the beam.
If the sound source is a plane, then it produces planar (plane) wavefronts and parallel rays. But if the source is a point or a small body, then it produces spherical (spherical) wavefronts and radial rays.
The sound that hits an obstacle can be reflected from it or absorbed by the obstacle. How much of the sound wave is reflected by the obstacle is called the reflection coefficient. In the following, we will assume that the obstacle completely reflects the sound. In this case, we say that the reflection coefficient is equal to 1.
The wave is reflected as if emanating from a specular source behind the reflecting surface. The law of reflection applies: the angle of incidence (measured from the vertical to the plane of incidence) is equal to the angle of reflection. Here we assume that the roughness of the reflecting surface is small enough compared to the wavelength so that the beam does not scatter.
The speed of sound depends on the substance through which the sound travels. It can be calculated using the equation:

We can see that the lower the compressibility  and the density
and the density 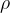 of the substance, the greater the speed
of the substance, the greater the speed 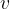 of sound. Due to low compressibility, we conclude that the speed of sound is highest in solids, followed by liquids and then gases.
of sound. Due to low compressibility, we conclude that the speed of sound is highest in solids, followed by liquids and then gases.
Instead of compressibility  we can also use modulus of elasticity
we can also use modulus of elasticity 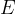 .
.
The modulus of elasticity is given as:

The compressibility  of a substance can be obtained from the expression:
of a substance can be obtained from the expression:
The modulus of elasticity 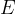 and compressibility
and compressibility  are inversely proportional. If we insert this into equation 1 above we get:
are inversely proportional. If we insert this into equation 1 above we get:

The speed of sound in air can also be calculated using equation (1) and using the gas laws. This is given as:

where 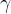 is the ratio of the specific heat capacity at constant pressure
is the ratio of the specific heat capacity at constant pressure 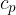 and the specific heat capacity at constant volume
and the specific heat capacity at constant volume 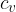 . In the case of diatomic molecules, of which air is mainly composed, its value is 1.40. This is called the adiabatic index of air.
. In the case of diatomic molecules, of which air is mainly composed, its value is 1.40. This is called the adiabatic index of air.
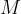 is the kilomolar mass of air (
is the kilomolar mass of air (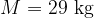 ),
), 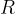 is the general gas constant and
is the general gas constant and 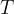 is the absolute temperature.
is the absolute temperature.
The table below shows the speeds of sound for some substances:
We can see that aluminum has the highest speed. This is due to the low density and compressibility of aluminum.
As an interesting fact, let us also mention that both longitudinal and transverse waves can spread through a solid. In this case, the speed of the transverse wave is approximately twice that of the longitudinal wave.
The speed of sound depends on the substance through which the sound propagates and on the temperature. We can read it from the table, or use one of the equations:
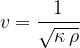
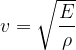
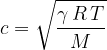
We see that in air, the speed of sound is proportional to the root of the absolute temperature. The proportionality constant is calculated from equation (4) and we get: