A tube, closed at one end, has a uniform area of cross-section. The tube contains some sand so that the tube floats upright in a liquid, as shown in the figure below.
When the tube is at rest, the depth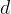 
of immersion of the base of the tube is 
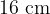. The tube is displaced vertically and then released. The variation with time 
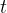of the depth 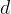of the base of the tube is shown in the graph below.
Use the graph to determine, for the oscillations of the tube,
the amplitude,
the period.
Calculate the vertical speed of the tube at a point where the depth 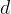is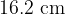 
.
State one other depth 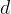where the speed will be equal to that calculated in (i).
.
.
.
.
