Define simple harmonic motion.
A tube, sealed at one end, has a total mass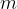 
and a uniform area of cross-section 
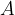. The tube floats upright in a liquid of density 
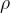with length 
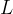submerged, as shown in Figure I below.
The tube is displaced vertically and then released. The tube oscillates vertically in the liquid. At one time, the displacement is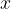 
, as shown in Figure II above. Theory shows that the acceleration 
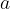of the tube is given by the expression
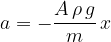
Explain how it can be deduced from the expression that the tube is moving with simple harmonic motion.
The tube, of area of cross-section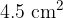 
, is floating in water of density 
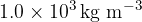. Calculate the mass of the tube that would give rise to oscillations of frequency 
.
