Personal collections
A hollow tube, sealed at one end, has a cross-sectional area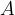 
of 
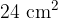. The tube contains sand so that the total mass 
of the tube and sand is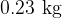 
. The tube floats upright in a liquid of density 
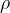, as illustrated in the figure below.
The depth of the bottom of the tube below the liquid surface is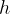 
. The tube is displaced vertically and then released. The variation with time 
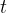of the depth 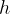is shown in the graph below.
Determine
the amplitude, in metres, of the oscillations,
the frequency of oscillation of the tube in the liquid,
the acceleration of the tube when 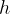is a maximum.
The frequency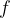 
of oscillation of the tube is given by the expression
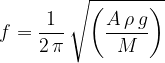
where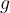 
is the acceleration of free fall.
Calculate the density 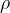of the liquid in which the tube is floating.
.
.
.
.
