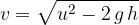Personal collections


Let's assume a body falls freely in an airless space and is therefore not hindered by the air resistance during its fall. The motion of this body is uniformly accelerated. Acceleration when falling is denoted by 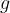 instead of
instead of  (from the word gravity). We call it gravitational acceleration, it can also be called free-fall acceleration.
(from the word gravity). We call it gravitational acceleration, it can also be called free-fall acceleration.
Gravitational acceleration is not constant but changes slightly. Let's list some factors that affect the magnitude of the (Earthly) gravitational acceleration:
latitude (it is slightly greater at the Earth's poles than at the equator);
altitude (with falling altitude);
soil composition (heavy minerals under the Earth's surface slightly increase 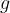 )
)
In our calculations, we will consider that the Earth's gravitational acceleration is equal to:
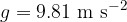
In the exercises, depending on the accuracy of the other data, we will round 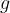 to a whole number (
to a whole number (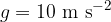 ), to one decimal place, (
), to one decimal place, (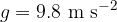 ) or to two decimal places as above.
) or to two decimal places as above.
Since a body moves in a vertical direction during a free fall or vertical throw, we will denote the distance covered by  (
(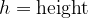 ) instead of
) instead of  .
.
The gravitational acceleration on the Earth's surface is the same for all bodies. Let us denote it by 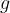 . Then a body falls freely with acceleration
. Then a body falls freely with acceleration 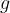 which is given as:
which is given as:
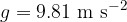
All equations and all graphs already known from the chapter, Uniformly accelerated motion are also applicable to the vertical motion under gravity, except that instead of the notation 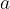 , we use the notation
, we use the notation 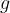 and instead of the notation
and instead of the notation  , we use
, we use  . The exact derivation of the formulas can be found in the chapter, Uniformly accelerated motion, we just repeat them here.
. The exact derivation of the formulas can be found in the chapter, Uniformly accelerated motion, we just repeat them here.
In free fall, the body has an initial velocity of 0 and then increases with the gravitational acceleration 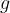 :
:
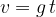
The graph of the change in velocity  against the time
against the time 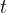 is as shown below:
is as shown below:
The final velocity  (Figure 1) when falling to the ground is:
(Figure 1) when falling to the ground is:
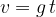
The height  that the body covers during the fall is the average speed
that the body covers during the fall is the average speed 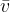 times the time
times the time 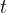 , or the area under the speed-time graph (the area of the region coloured green in Figure 1):
, or the area under the speed-time graph (the area of the region coloured green in Figure 1):
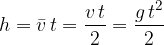
The time 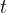 it takes to fall through the height
it takes to fall through the height  is:
is:
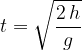
The final speed  after falling through the height
after falling through the height  is given as:
is given as:
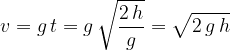
Let's repeat the formulas for free fall:
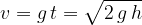
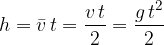
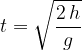
If we throw the body vertically downwards, it means we give it an initial velocity 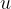 , then its velocity increases due to gravitational acceleration (see Figure 2). The velocity-time graph, formulas, and derivations are the same as for uniformly accelerated motion with an initial velocity
, then its velocity increases due to gravitational acceleration (see Figure 2). The velocity-time graph, formulas, and derivations are the same as for uniformly accelerated motion with an initial velocity 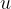 , only that we replace the acceleration
, only that we replace the acceleration 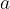 with
with 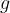 , and the distance
, and the distance  with
with  .
.
Just before the body falls to the ground, it reaches the final velocity  which is given as:
which is given as:
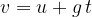
The fall height  is calculated by multiplying the average fall speed
is calculated by multiplying the average fall speed 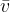 by the fall time
by the fall time 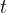 :
:
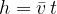
where the average speed 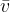 is given as:
is given as:
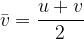
The distance  travelled can also be calculated as the area under the velocity-time graph:
travelled can also be calculated as the area under the velocity-time graph:
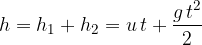
The final velocity, depending on the height from which the body falls, is given as:

When a body is thrown vertically downwards at an initial velocity 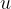 , the following general formulas apply:
, the following general formulas apply:
The final speed  of the body in time
of the body in time 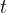 is given as:
is given as:
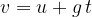
The height  of fall of the body in time
of fall of the body in time 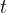 is given as:
is given as:
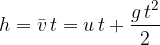
The final velocity  in terms of the height
in terms of the height  is given as:
is given as:

If the body is thrown vertically upwards by giving it an initial velocity 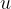 , the velocity of the body decreases, as it is acted upon by gravitational acceleration, which is in the opposite direction to the motion of the body. After a certain time
, the velocity of the body decreases, as it is acted upon by gravitational acceleration, which is in the opposite direction to the motion of the body. After a certain time 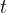 , the body reaches its maximum height
, the body reaches its maximum height  and stops.
and stops.
The motion of the body is uniformly decelerating as we have learned in the chapter, Uniformly accelerated motion, and the graph of velocity against time is given as:
The graphs and formulas we learned from the chapter, Uniformly decelerated motion (more precisely, the case where the body has an initial velocity that decreases with time) remain the same, we just replace the acceleration 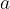 with
with 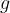 and distance
and distance  with
with  .
.
Formulas describing vertical upward throw:
The final speed  as a function of time
as a function of time 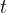 is given as:
is given as:
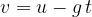
The time 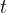 is given as:
is given as:
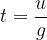
The height  of the body in time
of the body in time 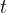 is given as:
is given as:

The maximum height  reached by the body is the area under the velocity-time graph and this is given as:
reached by the body is the area under the velocity-time graph and this is given as:
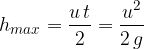
The initial speed 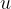 required to reach a certain height
required to reach a certain height  is given as:
is given as:

The final speed  of the body in terms of the height
of the body in terms of the height  is given as:
is given as: