Personal collections


When we lift weights, we do work, just like when we drive nails, lift hacks, dig with a shovel, or when we push a car - in all these cases, we do work. There are many more similar examples, all of which are characterized by the fact that we move something by the application of force. We can also find that the bigger the force we apply and the farther we move, the more the work we do. From here, we arrive at the following definition of work:
The work denoted by the letter  is defined as the scalar product of the constant force vector
is defined as the scalar product of the constant force vector  and the displacement vector
and the displacement vector  of the force.
of the force.
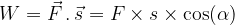
Where 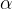 is the angle between the constant force and the direction of motion.
is the angle between the constant force and the direction of motion.
 is a constant force vector, which means that the magnitude of the force does not change, so we operate with a constant force.
is a constant force vector, which means that the magnitude of the force does not change, so we operate with a constant force.
 is the vector of the displacement of the force, which tells us where and by how much the force has moved.
is the vector of the displacement of the force, which tells us where and by how much the force has moved.
The unit of work is J (Joule). The work 1 J is the work done when a constant force 1 N moves a body (the point of application of the force) through a distance of 1 m:
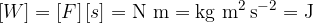
Take, for example, a woman pushing a shopping cart. When she pushes the shopping cart, she does work. If she pushes with a constant force  in the direction of motion -
in the direction of motion - 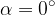 - and pushes the cart over a distance
- and pushes the cart over a distance  , the work done by the woman can be calculated using the formula above:
, the work done by the woman can be calculated using the formula above:

If we also have a child in the shopping cart, the child also pushes the cart with its weight, but perpendicular to the direction of motion - 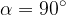 - and therefore does not do work, because if we calculate the work according to the formula above, we have:
- and therefore does not do work, because if we calculate the work according to the formula above, we have:
However, when pushing with a constant force at an angle 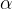 to the direction of motion, we use the formula to calculate the work done:
to the direction of motion, we use the formula to calculate the work done:
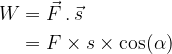
Let us look at the example of rotation shown in the figure below, where a tube wound on a reel is pulled with a constant force  . When the reel rotates through an angle
. When the reel rotates through an angle 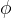 , the tube makes a distance
, the tube makes a distance 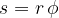 .
.
In our case, the direction of the force is tangential, which means that the angle between the force and the direction of rotation is 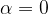 . Thus, the work can be calculated using the formula:
. Thus, the work can be calculated using the formula:
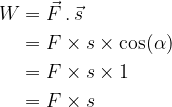
And if we consider that 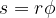 , we can write:
, we can write:

In the end, we wrote the work with torque 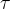 , since torque is a product of the force
, since torque is a product of the force 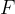 and the lever
and the lever  :
:
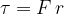
The work  of a force in rotation is therefore equal to the product of the torque
of a force in rotation is therefore equal to the product of the torque 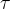 of the force and its angular displacement
of the force and its angular displacement 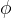 :
:
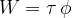
In a case where the force is not in the tangential, i.e., the angle between the force and the direction of rotation 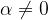 , only the tangential component
, only the tangential component 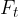 of the force is taken into account. Thus we get the formula:
of the force is taken into account. Thus we get the formula:

To define the work done by pressure, let's look at a lower piston, which presses on the liquid in a cylinder with a constant force 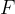 and in doing so moves through a distance
and in doing so moves through a distance  . The work done is :
. The work done is :

The force 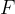 can also be expressed in terms of the pressure
can also be expressed in terms of the pressure 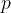 as:
as:
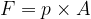
Where 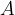 is the cross-sectional area of the piston (surface of the base surface) and therefore, we have:
is the cross-sectional area of the piston (surface of the base surface) and therefore, we have:

The product 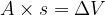 gives us the volume of the cylinder with the base area
gives us the volume of the cylinder with the base area 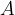 and the height
and the height  , which is equal to the volume of the liquid displaced. Thus we can write:
, which is equal to the volume of the liquid displaced. Thus we can write:
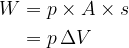
The work done by pressure is therefore equal to the product of the pressure under the piston and the volume of the displaced fluid.

In most cases, we are not really interested in what work the piston did to the liquid but rather, what work was done by the external force pushing the piston.
When we inflate a ball with an air pump, we are not interested in the work done by the piston, but how much work we do in pushing the piston. Therefore, we must take into account that the force 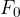 of air pressure also acts on the outside of the piston, which helps us to push:
of air pressure also acts on the outside of the piston, which helps us to push:

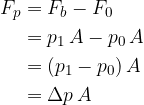
The work of the force with which we push the piston can thus be calculated by the equation: