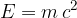The atomic nucleus is part of an atom. It can be imagined as a ball in which protons and neutrons are tightly packed together. Let's look at it in more detail.
The particles that make up atoms have already been described in the material, Atomic structure, here we only make a brief summary. Atoms are made up of:
protons, the number of which is denoted by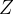 
and is called the atomic number,
neutrons, the number of which is denoted by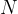 
, and
electrons,
The total number of protons and neutrons in the nucleus is called the mass number and is denoted by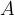 
. It tells us the approximate mass (weight) of the nucleus. Figure 1 shows the standard (chemical) notation of an element with its mass and atomic numbers:
Figure 1: Symbols denoting the helium element, which has two protons and two neutrons in the nucleus
The atomic number 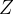tells us the number of protons in the nucleus, and the mass number 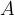tells us the total number of neutrons and protons in the nucleus.
The estimate of the radius of the nucleus is directly proportional to the third root of the mass number (that is, the total number of protons and neutrons):
Nuclei with the same number of protons and different numbers of neutrons are called isotopes.
Isotopes of a given element have very similar chemical properties, as these properties are determined primarily by the arrangement and number of electrons (which is equal to the number of protons). Isotopes thus differ from each other primarily in terms of mass (i.e. mass number 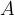), which, however, has no particular effect in most chemical reactions. The number of neutrons has a strong influence on what happens in the nuclei themselves, especially on their stability.
Hydrogen isotopes have proper names due to their importance. A nucleus with one proton and one neutron is called deuterium, and a nucleus with two neutrons and a proton is called tritium.
Isotopes of a given element differ in the number of neutrons.
The relative atomic mass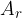 
of an element, which is sometimes listed next to each element in the periodic table, is the average mass of the different naturally occurring isotopes of that element. When reading 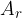from the periodic table of elements, we must be careful, because it is often expressed only as 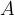, which is why it can be quickly replaced by the mass number 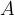. 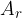is calculated using the formula:
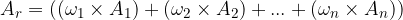
where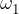 
, 
, ..., 
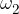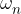are the proportions of the individual isotopes of the element in nature, and the 
, 
, ...., 
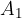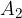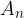are their mass numbers.
In the nucleus, all the protons are squeezed into a small space and although the positively charged protons (electrically) repel each other, the nucleus does not decay. The reason that the nucleus does not decay is that there are strong and attractive nuclear forces between the nucleons.
If we wanted to break the nucleus into individual free protons and neutrons, we would need an energy that would have to be greater than the binding energy of the nucleus. The magnitude of this energy varies between nuclei. The higher the binding energy, the more difficult it is to break the nucleus, and, as a result, such nuclei are more stable.
If the binding energy is divided by the number of nucleons, we get the average energy with which a single nucleon is bound to the nucleus. This energy is called the specific binding energy and is a measure of the stability of the nucleus. Nuclei with a higher specific binding energy are more stable than nuclei with a lower one.
The binding energy of a nucleus is the energy that would be required to split the nucleus into free protons and neutrons.
The specific binding energy of a nucleus is the average energy with which individual nucleons are bound to the nucleus.
The following figure shows a graph of specific binding energies for different nucleons:
Figure 3: Specific binding energies of different nuclei
From the graph, we can see that the specific binding energy - when we move from lighter nuclei to heavier ones - first increases, reaches its peak at the nuclei around nickel and iron, and then, when we start moving towards heavier nuclei, it starts to fall.
The binding energy of a nucleus is determined with the help of the mass defect of the nucleus. If:
we measure the total mass free protons and neutrons in a nucleus, and
we measure the mass of the nucleus of the same number of protons and neutrons,
we find that the mass of the nucleus is less than the total mass of the free protons and neutrons. This difference in masses is called the mass defect.
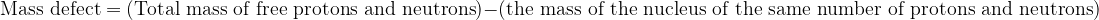
We express this mathematically as:
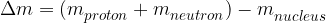
This fact violates the law of conservation of mass, which is one of the basic laws of classical physics. But in nuclear physics, this conservation law does not apply. Why?
The change in mass is related to the energy released or consumed during the reaction. The conversion of mass into energy and vice versa is described by the equation:
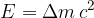
where 
is the speed of light. This is the famous Einstein's energy equation.
The mass defect of the nucleus is therefore the mass that is converted into the binding energy of the nucleus. Therefore, the nucleus is lighter than free protons and neutrons. This is also the energy that must be brought in if we want to split the nucleus again.
The mass of the nucleus is not equal to the sum of the masses of the protons and neutrons that make up the nucleus. Such a mass difference is called a mass defect. We explain the mass defect using Einstein's energy equation:
