Personal collections


The word entropy has its origin in classical Greek and means reversal or change.
Let us observe changes in nature and take the whole of nature as a single system. With the help of work, man changes the environment: he builds a house, tidies up an apartment, regulates the riverbed, builds a factory. Imagine leaving the result of the work to nature after the work is finished. After a long enough time, the condition will be the same again as it was before his intervention. The house and the factory will collapse, and the river will flow again along the riverbed of its choice. At first glance, the situation will be as if there were no human influence.
Will the situation really be exactly the same? The fact that he had to do work to arrange the surroundings, for which, e.g. needed his physical strength, construction machinery, etc., tells us that the condition will not be exactly the same as before the procedure. If nothing else, the work changed the internal energy of the system: the environment found itself at a higher temperature than before.
In physics, the measurement of such changes is denoted by a quantity called entropy; for the human intervention in the environment described above, we say that we increased the entropy of the system. What exactly is entropy that we will learn in this material? For now, it is enough to know that entropy is a measure of the accumulated changes that have occurred in a system. The notation for entropy is 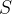 .
.
Spontaneous changes in nature tend to disorder, to the greatest possible entropy. With each of our interventions in the environment, where we try to reduce the entropy, we cause the final entropy to increase again after spontaneous changes, and this by more than we managed to reduce. Entropy as a result of accumulated changes can never be reduced; the change in entropy is greater or, ideally, at most equal to zero.
Let’s look at the example above again and take the motion of one ant. The probability that the ant will find itself at the same point again is quite high. However, the probability that all ants will find themselves at the starting point at the same time is extremely small. But even though it is extremely small, it is still a possible situation.
From what has been said, we can deduce the following:
entropy is a statistical variable in which we use probability calculus;
entropy can be at most 0 (ants gather again at starting points). An entropy less than 0 in this case doesn’t even make too much sense, namely, what would it mean for ants to be “more” orderly than they were in the beginning?
If changes are observed at the macroscopic level, it can be recorded with sufficient certainty that spontaneous reactions take place in only one direction (such as heat flow). Spontaneous reactions that occur in only one direction are called irreversible or irreversible changes.
We also know reversible or reversible changes. These are rare, but important because they maintain the entropy of the system (as opposed to irreversible changes that increase the entropy of the system).
The changes will be observed in a system that is thermally insulated from the surroundings. In this way, we will observe an autonomous system that gives us meaningful results. But what would have happened if this condition had not been set? If the observed system were not thermally insulated from the surroundings, heat could be transferred from the system to the surroundings.
And if this environment were, let's say, at a lower temperature, this would reduce the entropy of the observed system. But this result would be due to the fact that we did not take the surroundings into account in our observations. We would get an erroneous result resulting from inconsistent observation; namely, the real result in observing the observed system together with the surroundings would be an increase in entropy.
The concept of entropy is used in many fields of physics and other fields where we are dealing with a large number of events and where probability calculus applies. In this chapter, we will limit ourselves to the area of heat only.
Irreversible and reversible changes
Most changes in nature are such that they can only occur spontaneously in one direction. We call them irreversible changes. Rare changes, however, take place in the same way in both directions. We say they are reversible. In understanding entropy, it is very important to know how to distinguish reversible changes from irreversible ones. Irreversible changes are listed below:
It is much harder to achieve reversible changes than irreversible ones. All reversible changes are made very slowly without friction or resistance. By saying that reversible changes occur slowly, it means that at all times, all parts of the observed system are in thermal equilibrium.
Most changes in nature are irreversible. Reversible changes can be achieved only in rare cases and with careful execution of the experiment.
The conditions for a reversible change are:
The change can be reversed so that the body is finally in the same state and position as it was at the beginning
Intermediate states between transitions in one direction and another are exactly the same: on the contrary, the same speed, the same force, the same temperature, and so on. It must seem to us as if we were just turning the film in the opposite direction when reversing the change.
There is no friction or air resistance during the change.
Changes take place slowly so that all parts of the system are always in thermal equilibrium during the change.
Let us recall the [First law of thermodynamics | first law of thermodynamics], which states that the change in internal energy is equal to the work put in and the heat added:
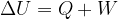
This law says nothing about the direction of heat flow. In principle, it also allows for the possibility of heat flowing from a colder body to a warmer body. A colder body thus cools down even more (its internal energy decreases), and a warmer body heats up even more (its internal energy increases).
We know from experience, however, that such a flow is not in itself possible, or that it is very unlikely. We suspect that there is a new law that describes this phenomenon. This law really exists, and we call it the 2nd law of thermodynamics or the entropy law. We got to know it in the simplest form already in the introduction:
If the body is thermally insulated, it can no longer be restored to its original state after an irreversible change has been made. In doing so, the entropy of the body increased.
But what is entropy, and how do we calculate it? It is most easily known by means of the gas equation.
Recall the gas equation, which relates the three main thermodynamic variables: pressure 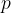 , volume
, volume 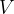 , and temperature
, and temperature 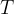 :
:
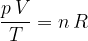
The quotient on the left side of the equation is constant for a given amount of gas. It is equal to the product of the number of kilomoles 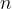 and the general gas constants
and the general gas constants 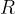 .
.
So far (on the ideal gas), we have considered changes where one of the variables was a constant. These were:
isothermal changes (constant temperature),
isobaric changes (constant pressure),
isochoric changes (constant volume)
Now, however, we will allow the pressure, volume, and temperature to change at the same time.
In the same graph (Figure 2), we draw:
isothermal changes: these are changes that describe the dependence of pressure on volume at constant temperature (red lines in Figure 2);
adiabatic changes: these are changes where the gas is allowed to heat up during compression and cool down during expansion (blue lines in Figure 2).
The curves denoting the adiabatic change on the graph are called adiabat. The word adiabat comes from classical Greek and means impassable. It means that the gas is thermally insulated, so the heat cannot pass into the surroundings.
On adiabats, the temperature rises if the volume decreases and the pressure increases, and vice versa: if the volume increases and the pressure decreases, the temperature decreases.
At a normal air pressure of 1 bar, the temperature points on the isotherm and adiabat are identical. They represent the (initial) temperature of the gas before it is compressed or expanded. On adiabats, it is considered that:
the gas heats up during compression. This means an additional higher pressure, so the adiabat, for pressures greater than 1 bar, is steeper than the isotherm.
during expansion, the gas, at a pressure below 1 bar, cools further, so the position of the adiabat there is lower than the isotherm.
We have already established (see examples of reversibility) that changes under certain conditions (slow changes, thermally insulated cylinder with low heat capacity, no friction between piston and cylinder) - and are indicated by an adiabat - are reversible. There is no change in entropy for reversible changes. Adiabats are therefore lines where the entropy 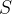 is constant.
is constant.
A family of curves with a constant temperature is obtained by varying the temperature of the gas. But how do we get the adiabat family?
One possibility is to perform an irreversible change on the gas and thereby increase its entropy. But computing with irreversible changes is quite complicated. Therefore, the problem is avoided by adding heat  to the gas at a certain temperature
to the gas at a certain temperature 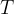 (see Figure 3). This gas changes the entropy by:
(see Figure 3). This gas changes the entropy by:

We arrived at an adiabatic with slightly higher entropy. However, we can also make a change in the other direction: we take away the heat from the gas and thus reduce its entropy. We are talking about reversible adiabatic changes.
Equation (1) can be arrived at empirically or by mathematical derivation. We found that the quotient 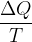 is independent of which path and at which temperature we pass between adiabats. Figure 3 shows an example of isobaric (at constant pressure
is independent of which path and at which temperature we pass between adiabats. Figure 3 shows an example of isobaric (at constant pressure 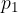 ) and isochoric (at the same volume
) and isochoric (at the same volume 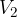 ) transitions between two nearby adiabats.
) transitions between two nearby adiabats.
In isobaric and isochoric transitions, the change in entropy is the same, as we arrive at the same adiabatic with higher entropy:
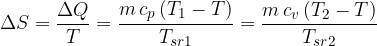
The same is true for other transitions between adiabats. No matter by which route and at what temperature they are performed, we always come to the same adiabat (note: more about 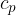 and
and 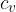 in the material (first law of thermodynamics).
in the material (first law of thermodynamics).
For adiabats, the entropy is considered to be constant.
Any irreversible process results in a transition to an adiabatic with higher entropy.
An adiabatic with a higher entropy can also be reached by allowing the transfer of heat  at a certain temperature
at a certain temperature 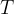 . Among the adiabats adjacent, where the temperatures differ only slightly between the transition points, we can calculate the change in entropy:
. Among the adiabats adjacent, where the temperatures differ only slightly between the transition points, we can calculate the change in entropy:

It does not matter at what temperature or by which path we reach a nearby adiabatic with higher entropy.
The circular change means that our end point of the journey along the graph is equal to the starting point. If we travel exclusively through adiabats, we call this an adiabatic circular change.
By adding and subtracting heat to an ideal gas, a reversible adiabatic circular change can be achieved. Let us observe such a circular change between adiabats in Figure 4:
Let's describe the process:
Transition between point 1 and 2
From adiabatic with a lower entropy, we switch to an adiabatic with a slightly higher entropy by supplying heat 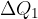 to the gas at a certain temperature
to the gas at a certain temperature 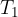 . At the same time, the gas temperature also increased slightly. Since the heat input was small, the temperature change was also small, so we can calculate with some mean temperature at the transition
. At the same time, the gas temperature also increased slightly. Since the heat input was small, the temperature change was also small, so we can calculate with some mean temperature at the transition 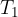 .
.
Transition between point 2 and 3
The gas expands adiabatically and does the work.
Transition between points 3 and 4
The entropy of the gas is reduced by taking the heat 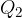 from it at a medium temperature
from it at a medium temperature 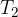 . At the time of removal, we therefore temporarily suspended the thermal insulation of the gas, removed the heat from the gas, and returned to the original adiabatic.
. At the time of removal, we therefore temporarily suspended the thermal insulation of the gas, removed the heat from the gas, and returned to the original adiabatic.
Transition between point 4 and 1
The gas is compressed adiabatically. In doing so, we perform work that is slightly smaller than the work in the span between points 2 and 3. The difference between the work emitted by the gas at the transition 2 - 3 and the work received by the gas at the transition 4 - 1 is useful work 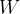 , which can be used in the case of heat engines. It is proportional to the area of the loop in Figure 3.
, which can be used in the case of heat engines. It is proportional to the area of the loop in Figure 3.
We emphasize once again that this is a reversible adiabatic change, where entropy is preserved after the path is completed. With each additional irreversibility, the entropy can only increase:
A Carnot circular change is a circular change that travels partly along an isotherm and partly along an adiabatic one. It is important because Carnot’s circular change is the basis for understanding heat engines.
Imagine a transition at a constant temperature (after isotherms). If we want circular changes, we need two transitions:
at a higher temperature on adiabatic with higher entropy
and back at a lower temperature to the original adiabatic.
Figure 5 shows the Carnot circular change, which describes the operation of a heat engine based on adiabatic reversible circular changes of an ideal gas. As we have mentioned several times, the machine must operate slowly, without friction, with a small heat capacity of the cylinder and piston, and in a thermally insulated environment.
Figure 5 shows the same isotherms and adiabats as those shown in Figure 2. Describe the circular change as indicated in the Figure:
Amendment 1 - 2
The gas at a higher temperature 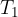 isothermally expanded by adding heat
isothermally expanded by adding heat 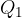 . The volume increases and the pressure decreases.
. The volume increases and the pressure decreases.
Amendment 2 - 3
The gas is expanded adiabatically. For this purpose, it is thermally insulated so that its temperature drops to 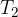 .
.
Amendment 3 - 4
The gas is compressed isothermally at a lower temperature 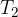 .
.
Amendment 4 - 1
The gas is compressed adiabatically to reach the initial temperature 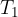 again.
again.
Now, let's describe this circular change mathematically:
Isothermal change 1- 2
In the case of isothermal change, the heat input is equal to the work done by the gas:
Isothermal change 3 - 4
In this change, we do the work and compress the gas, so the sign is negative. The result is similar to what we got earlier:
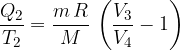
Adiabatic change 2 - 3
In the case of adiabatic change,  is constant (since the system is thermally insulated), according to the first law of thermodynamics, therefore the change in internal energy is equal to the work done:
is constant (since the system is thermally insulated), according to the first law of thermodynamics, therefore the change in internal energy is equal to the work done:
Adiabatic change 4 - 1
The derivation is similar to that for adiabatic change 2 - 3. We get:
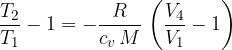
Let's write again the equation obtained in adiabatic variation 4 - 1:
Now, let's write down again the equation we got at the transition 3 - 4:
We have obtained an important connection that we will use to our advantage when observing heat engines. In doing so, we emphasize once again that all changes must be very slow, so that at any given moment the gas is in thermal equilibrium.
The same equation can also be arrived at as follows: at the end of the circular change, all thermodynamic variables have the same value. The change in entropy is zero:
For a Carnot circular change, the ratio of heat given off or received by the heat engine during the circular change is considered to be equal to the ratio of the temperatures at which these changes take place:
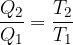
In the chapter Heat engines, we wrote the equation for the efficiency of a heat engine as:
We concluded that the efficiency of a heat engine operating after reversible Carnot changes is the same:
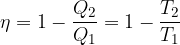
Let's consider a process which is not completely reversible due to piston and cylinder friction or any other factor:
In this case:
The equation is inserted into the equation for the efficiency of the heat engine, and we get:
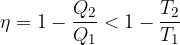
The same could be done for other heat engines: a refrigerator and a heat pump.
The efficiency of heat engines is:
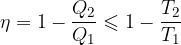
The coefficient of performance of refrigeration machines is:
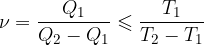
The coefficient of performance of heat pumps is:
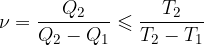
The smaller sign is used when the changes are irreversible.
Transitions between two states
We will now no longer speak of transitions between two adiabats, but generally between two states with different entropy. We write again the equation for the change in entropy; recall that the equation does not only apply to an ideal gas, but to any change in entropy:
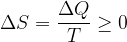
If the temperature difference between the two states is large, we can no longer take the mean transition temperature 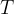 as we did in the previous chapter. In this case, divide the transition into several sections with medium temperatures
as we did in the previous chapter. In this case, divide the transition into several sections with medium temperatures 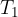 ,
, 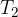 , ...,
, ..., 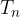 , add heat
, add heat 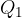 ,
, 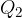 , ...,
, ..., 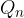 in each section. To this, we form quotients representing small fractions of entropy and add them up:
in each section. To this, we form quotients representing small fractions of entropy and add them up:

In doing so, we intuitively followed the rule that entropies add up.
This section is for students who have already learned the basics of integration. Everyone else can skip it without affecting the understanding of entropy.
Water entropy
The table for internal energy 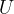 and entropy
and entropy 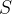 for
for 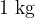 of boiling water and steam at saturated vapor pressure is given. The reference value of internal energy
of boiling water and steam at saturated vapor pressure is given. The reference value of internal energy 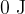 and entropy
and entropy 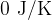 is selected at a temperature of
is selected at a temperature of 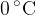 , where the saturated vapor pressure is
, where the saturated vapor pressure is 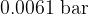 .
.