Personal collections


A boy pushes a cart up an inclined plane. He exerts a force on the cart that causes the cart to move. He realizes that it is too heavy, so he calls a friend for help. Now they are pulling with a double force since the forces of both friends' hands are parallel and act in the same direction.
A child kicks a ball. With the force of his foot, he causes the ball to fly towards the goal. We hang a weight on an elastic rope. The rope stretches. A plane flies through the air. A stone falls to the ground. All these phenomena and many more are the results of the action of force.
Forces can also act in such a way that the body is stably at rest (e.g. a pencil is stably at rest on a table). This does not mean the absence of forces, but that the forces are in balance. Their total impact on the body is zero. We also say that their sum or resultant is equal to zero and therefore the body is in a stable state - in equilibrium.
Force is a concept that is described in several materials:
the materials, Force and acceleration and Forces in a circular path describe the force on a moving body;
in Friction and Bonding Force we learn about forces that resist movement;
Torque describes turning effect of force;
in the material Gravitational Field, we learn about Newton's law of gravity and Kepler's laws about the movement of celestial bodies;
But we will get to know the force gradually. In this chapter, we will focus on the basic concepts related to force: we will establish that it is a vector and consolidate some mathematical knowledge about vectors. In this way, we will also learn to calculate with forces.
Force is a vector physical quantity. The symbol for force is 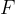 and the unit is
and the unit is 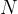 (Newton).
(Newton).
In physics, we determine the existence of a force indirectly by observing its effect on the body on which it acts. A force can act on a body by:
changing the speed of motion of the body - see Force and acceleration,
changing the direction of motion of the body - see Forces in a circular path,
deforming the body - see Newton's third law of Motion.
The effect of force on a body can be:
through direct contact between the force and the body (contact force).
through indirect contact between the force and the body (force field). We all know the force of gravity 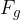 . This acts at a distance and is the result of the attractive force between the body and the Earth (see the chapter, Gravitational Field).
. This acts at a distance and is the result of the attractive force between the body and the Earth (see the chapter, Gravitational Field).
Since the force is a vector, it has - like every vector - its point of contact, magnitude, and direction (see figure 1):
the point of contact of a force is the point through which the force acts on a body;
the magnitude of the force is represented graphically in such a way that the length of the directed line is proportional to the magnitude of the force;
the direction of the force is marked graphically with an arrow.
In certain cases, the force can have the same effect on the body even if it has different grips (points of contact). Let's take a closer look at this with a concrete example:
Since the vector nature of force is extremely important for understanding and calculating forces, we will summarize part of the mathematical knowledge about vectors below. We will learn:
what the parallel displacement of a force vector mean and why we use it in graphical displays and sum calculations,
how forces are added vectorially,
what an opposing force is and how we use it for (vector) subtraction of forces,
how to resolve a force into components, and
what equilibrium of forces is.
Force is a vector. It has its own:
magnitude,
direction, and
point of contact or grip or line of action.
A point of contact is a point through which a force acts on a body.
We learn about force indirectly, namely by determining its influence on a body. It can change the speed or direction of motion of the body or deform it. A force on a body can act:
in direct contact with the body (contact force); or
far away (force field).
Various calculation operations can be performed on forces, as well as on all vectors (see Operations with vectors). We limit ourselves to the following operations:
parallel displacement,
addition of forces, and
subtraction of forces.
When adding (or subtracting) forces, we get the vector sum of forces. We also call it the resultant.
When we add forces, we must add them vectorially. The direction and magnitude of the forces must be considered. We can use a graphical approach, knowledge of geometry, or vector calculus. The result we get is called the sum or resultant of the forces.
When summing forces, we can make it easier by applying the knowledge of the parallel movement of forces. This mathematical vector rule states that a vector is preserved if it is moved parallel to it in a plane or space.
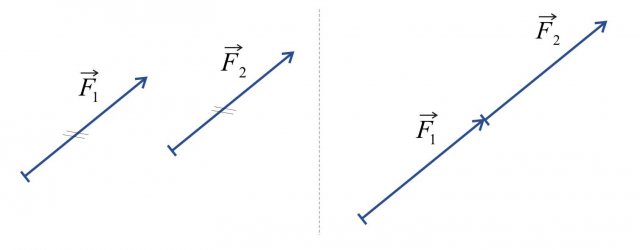
Figure 3: The two vectors on the left (or just one of them) can be moved in parallel e.g. by placing both along one axis as shown on the right
If the two vectors have the same magnitude and direction, their equality is indicated by two equal and parallel lines (Figure 3, left). In this case:
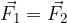
The rule is advantageously used when adding and subtracting forces in parallel along the plane.
In the case of parallel displacement, the grip of the vector is not preserved. Therefore, it is only a mathematical tool that we use when adding forces. After the summation operation is performed, the vector is placed again in the initial grip.
Two forces are opposite if they are equal in magnitude and opposite in direction. In this case, they cancel out on the outside. This means that they do not affect the surroundings, as we learned in the introductory chapter. Their sum or resultant is equal to zero.
The forces in Figure 4 are equal in magnitude but opposite in direction. Their sum is therefore equal to zero:
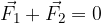
or:

A negative force with respect to the original force is obtained by keeping the magnitude of the force vector but directing it in the opposite direction. Consequently, if we add a force and its opposite force, their resultant is equal to 0.
In the chapter, Force and acceleration, we learned that if two opposing forces act on a body, the body is at rest.
When adding several forces, we add individual forces to each other, which we call components. The sum of the components gives us a new force, which we call the resultant. It is characteristic of the resultant that its effect on a body is the same as the effect of all components on the body together.
When searching for the resultant in practice, we always draw a sketch, which is not only intended for solving problems graphically but also makes it easier for us to visualize when calculating with forces.
We graphically add forces in two ways:
using the parallelogram rule; and
using the polygon of forces.
Let's take two forces with the same grip as shown in Figure 5 below:
The two forces are added according to the parallelogram rule using the following procedure:
We move the forces that we intend to add up in parallel so that they have the same point of contact (blue arrows).
We draw a parallel to the first force and move it to the end of the second force (green arrow).
In the same way, we draw a parallel to the second force and move it to the end of the first force (green arrow).
The blue arrows together with the green parallels form a parallelogram. We connect the point of contact of both forces with the opposite vertex and get the sum or resultant (red arrow).
If more forces are given, the forces can be summed up by taking the following procedure:
We draw the first force (it could be any of the forces);
then we place the second force (again, it could be any of the remaining forces after the first) in parallel and with its starting point at the end of the first force;
we take any third force and transfer it parallel to the end of the second force.
We repeat the process until the last force.
We then connect the beginning of the first and the end of the last force and get the resultant. The resulting sum of vectors/forces is:
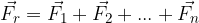
The vector of the resultant can be moved again with a parallel displacement.
The forces are added graphically with the help of the parallelogram rule or with the help of the polygon of forces.
Parallelogram rule
With this rule, we can add only two vectors at the same time. We draw a parallel to the first vector and place it at the end of the second vector. We do the same with the second vector. We get a parallelogram. The diagonal of the parallelogram is the resultant.
Polygon of forces
All forces have the same grip, e.g. in the coordinate origin. We move the forces in parallel and in such a way that the beginning of the second force is at the end of the first force, the beginning of the third force is at the end of the second force, etc. Finally, we connect the beginning of the first force and the end of the fourth force and get the resultant.
We subtract the force 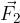 from the force
from the force 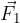 by adding the opposite force to it (see Figure 8):
by adding the opposite force to it (see Figure 8):
We move the force 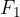 in parallel and to the place where we will draw the construction.
in parallel and to the place where we will draw the construction.
We must write the force 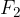 with the minus (-) sign and the direction. With this, we have reversed the sign of the force vector and got the vector
with the minus (-) sign and the direction. With this, we have reversed the sign of the force vector and got the vector  .
.
The negatively signed (and oppositely directed) force vector 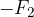 is moved in parallel and added to the end of the vector
is moved in parallel and added to the end of the vector 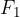 .
.
We then connect the beginning of the first vector and the end of the second vector and get the resultant:
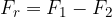
Let's draw the subtraction procedure:
Parallel forces are added in the same way as for a polygon. We move the forces in parallel and always place their starting point at the end of the previous force (making sure to change the direction of the negative force). Finally, we connect the beginning of the first force and the end of the last force. We get the sum or the resultant.
In Figure 9, we add two positive forces 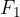 and
and 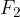 and then add the negative force
and then add the negative force  . We connect the beginning
. We connect the beginning 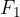 and the end
and the end  and get the resultant:
and get the resultant:

Resolving a force 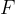 into its components is the reverse of the parallelogram addition of forces. In the parallelogram addition (in the plane), two forces are added into a single one while in the resolution of forces, a single force (in the plane) is resolved into two components. Before we resolve a force into components, we must specify the directions of the components.
into its components is the reverse of the parallelogram addition of forces. In the parallelogram addition (in the plane), two forces are added into a single one while in the resolution of forces, a single force (in the plane) is resolved into two components. Before we resolve a force into components, we must specify the directions of the components.
Let’s look at an example of force resolution.
The forces acting on a selected body are in equilibrium when their resultant equals zero. Then the body is at rest or moving uniformly and in a straight line (see the chapter, Force and acceleration). Whenever we observe a stationary body in nature, we know that all the forces acting on the body are in equilibrium. Their resultant is equal to zero.
We have already seen that two equally large and opposite forces have a resultant equal to zero. If such a pair of forces acts on a body, the body is in equilibrium.
Let us now observe the equilibrium with the polygon of forces. The forces are in equilibrium if the polygon of forces is completed in such a way that the end of the last force exactly coincides with the beginning of the first force (see Figure 11).
Forces acting on a selected body are in equilibrium if their resultant is zero. At that time, the body is at rest or moving uniformly and in a straight line.
This part is intended only for students who have mastered trigonometric functions. Otherwise, the exercises related to this chapter can be solved even without knowledge of trigonometry, but only if we have specified vectors that are inclined at "perfect" angles such as 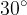 ,
, 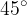 and
and 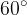 with the abscissa axis. In this case, we can also use the knowledge of geometric figures when resolving vectors into components, e.g. square and equilateral triangle.
with the abscissa axis. In this case, we can also use the knowledge of geometric figures when resolving vectors into components, e.g. square and equilateral triangle.
Let there be given vectors in the Cartesian coordinate system with the grip point at the coordinate origin and we want to resolve each of the individual vectors into two components:
the component 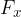 acting in the direction of the x-axis, and
acting in the direction of the x-axis, and
the component 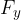 acting in the direction of the y-axis.
acting in the direction of the y-axis.
For ease of understanding, let's take the example of two vectors; the procedure for calculating the resultant of several vectors is similar.
Vectors (arrows in Figure 13) can be summed in the Cartesian coordinate system by first resolving them into components in the direction of the x and y-axes (dashed lines in Figure 13).
The components can generally be written using the sine and cosine functions:
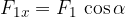
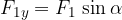
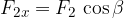
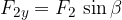
The resultant vector has an x-component which is the sum of the x-components of the individual vectors and a y-component which is the sum of the y-components of the individual vectors:
The components of the resultant vector are written as the sum of the corresponding components of the basic vectors:
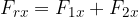
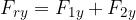
The absolute value of the resultant vector is obtained according to the Pythagorean theorem:

We obtain the direction of the resultant vector using tangent function: