Personal collections


Thermodynamics is a special branch of physics, which is called heat for short. It studies the thermal equilibrium, of thermally insulated systems, energy theorems, change of states - that is, changes in the aggregate state, etc. We will learn more about this below.
In the following subsections, we will:
learn what internal energy is;
learn the law of thermodynamics, which connects internal energy, heat, and temperature;
learn about thermodynamic variables and how we measure temperature.
learn about the types of physical systems (open, closed, and isolated systems).
expand the existing knowledge about energy theorem.
In this material, we will add internal energy to kinetic energy, potential energy, and elastic energy. Let's demote it with:
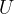
Let's list some forms of internal energy:
Kinetic energy due to the movement of molecules of matter.
Potential energy generated by intermolecular forces.
Internal energy in molecules and atoms.
Potential energy due to intermolecular forces will not be considered in this chapter. This force is small in sufficiently diluted gases, which we will treat as an ideal gas in which the intermolecular force is neglected. Also, we will not consider the internal energy in molecules and atoms. Molecules can be imagined as rigid balls that collide with each other and against the wall of the container. The entire internal energy will therefore be contained in the disordered motion (kinetic energy) of the molecules.
To study thermodynamics, we use quantities called thermodynamic variables. The basic thermodynamic variables are:
volume,
pressure,
mass,
temperature.
We are familiar with the first three, but we will learn about the fourth, temperature, in this subsection. We will also learn about the connection between heat and temperature.
Absolute temperature is used in thermodynamics. It is denoted by  and the unit is
and the unit is 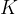 (Kelvin). A temperature of zero Kelvin is called absolute zero. A lower temperature than absolute zero is not possible.
(Kelvin). A temperature of zero Kelvin is called absolute zero. A lower temperature than absolute zero is not possible.
From everyday life, we are used to the Celsius temperature scale with a unit 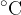 (degrees Celsius). In most cases, when it comes to absolute temperature or temperature difference, we will use the unit
(degrees Celsius). In most cases, when it comes to absolute temperature or temperature difference, we will use the unit 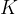 .
.
Let's take a look at the comparison of the two scales:
Both scales are numerically shifted by 273 units. We convert the temperature between Kelvin and Celsius as follows:
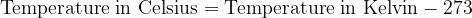

For calculations where we only have to enter the temperature difference 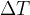 , the temperature difference in Kelvin is numerically the same as the temperature difference in degrees Celsius.
, the temperature difference in Kelvin is numerically the same as the temperature difference in degrees Celsius.
The most important thermodynamic variables are pressure 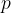 , volume
, volume 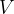 and temperature
and temperature  .
.
Temperature  is the thermal state of a body expressed in Kelvin (
is the thermal state of a body expressed in Kelvin (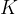 ). The Celsius scale is obtained by subtracting the Kelvin number of 273.
). The Celsius scale is obtained by subtracting the Kelvin number of 273.
If we only observe the temperature difference, we can use the Celsius or Kelvin scale, since the temperature differences are numerically the same.
To avoid confusion in the notations, the temperature in Kelvin is denoted by  , and the temperature in Celsius is denoted by
, and the temperature in Celsius is denoted by 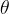 .
.
Accurate temperature measurement is made possible by a gas thermometer that works on the basis of the gas equation. This says that for a certain amount of gas, the product of pressure 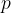 and volume
and volume 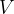 is proportional to temperature
is proportional to temperature  . Let the proportionality constant be
. Let the proportionality constant be 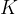 , we have:
, we have:
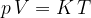
A gas thermometer can be used to measure temperature by measuring pressure at constant volume or volume at constant pressure. The temperature is calculated using the formula:
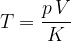
The factor 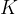 is explained in detail in the chapter, gas equation.
is explained in detail in the chapter, gas equation.
The gas thermometer is used as a measuring standard (official benchmark), but it is quite unsuitable for practical temperature measurement. In practice, we use thermometers that take advantage of the dependence of the extension of substances on temperature (mercury thermometer, bimetallic thermometer, or an electronic thermometer). All of them are characterized by the fact that they are useful only for a limited temperature range of measurements.
The thermometers in the image above are:
the classic thermometer (Figure 2, left), uses the expansion of a liquid (e.g. colored alcohol, mercury, etc.) with temperature.
the bimetallic thermometer (Figure 2, middle), contains two welded sheets of metal that expand differently due to temperature. The result of different extensions is the bending of the leaflets, which is proportional to the temperature.
the electronic or digital thermometer (Figure 2, right) can be:
temperature-dependent electrical resistor; in this case, we measure the current through the resistor at a constant voltage. The current depends on the temperature  .
.
thermocouple; in this case, we have two joints of two metals. If the joints are at two different temperatures, an electrical voltage is created between the joints, which depends on the temperature difference.
Heat is the movement (kinetic energy) of molecules in gases and liquids or the oscillation of molecules in a solid.
The movement of molecules is easiest to observe in a liquid. We put tiny floating granules in the liquid. Due to the collisions of the moving molecules of the liquid, the granules move in a disorderly manner along some kind of zigzag tracks. The higher the temperature of the liquid, the faster the movement. This motion is called Brownian motion.
There is a similar movement in gases. In solids, kinetic energy is manifested in the oscillation of molecules around the free space available to the molecule.
When we heat a substance, we add heat quantity 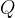 and thereby increase the kinetic energy of the molecules. Through collisions, molecules can transfer kinetic energy from a warmer to a colder substance with which it is in thermal contact. In this case, the warmer substance cools (gives off heat, and the speed of the molecules decreases) and the colder one heats up (receives heat, and the speed of the molecules increases). If the two substances are in a thermally insulated container, sooner or later, thermal equilibrium is established: all molecules have the same kinetic energy - they are at the same temperature.
and thereby increase the kinetic energy of the molecules. Through collisions, molecules can transfer kinetic energy from a warmer to a colder substance with which it is in thermal contact. In this case, the warmer substance cools (gives off heat, and the speed of the molecules decreases) and the colder one heats up (receives heat, and the speed of the molecules increases). If the two substances are in a thermally insulated container, sooner or later, thermal equilibrium is established: all molecules have the same kinetic energy - they are at the same temperature.
Heat 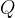 is the energy that causes a change in the speed (and thus the kinetic energy
is the energy that causes a change in the speed (and thus the kinetic energy 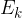 ) of the molecules.
) of the molecules.
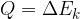
The notation for heat is 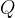 , and the unit is the same as for all other types of energies: Joule with the notation
, and the unit is the same as for all other types of energies: Joule with the notation 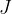 .
.
Heat is transferred from a warmer to a colder body through thermal contact due to the collisions of molecules.
In the chapter on thermodynamics, we will consider only the kinetic energy due to the thermal motion of molecules as internal energy.
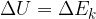
It is easiest to study if we observe the movement of molecules in an ideal gas. This is a gas that is sufficiently dilute that intermolecular forces can be neglected. Let's imagine the molecules as rigid balls that move randomly in space and elastically collide with each other against the wall of the container.
The kinetic energy 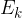 of a molecule in an ideal gas is proportional to the absolute temperature
of a molecule in an ideal gas is proportional to the absolute temperature  . The proportionality factor is the Boltzmann constant.
. The proportionality factor is the Boltzmann constant.
The kinetic energy 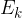 of a molecule in an ideal gas is proportional to the absolute temperature
of a molecule in an ideal gas is proportional to the absolute temperature  .
.

where 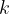 is the Boltzmann constant which is given as:
is the Boltzmann constant which is given as:
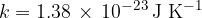
If we have 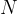 molecules of an ideal gas in a closed space, the total kinetic energy of all molecules is - see equation (1):
molecules of an ideal gas in a closed space, the total kinetic energy of all molecules is - see equation (1):
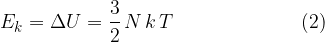
The number of molecules 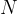 is rather expressed in terms of the mass
is rather expressed in terms of the mass 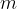 - see Atomic and molecular masses:
- see Atomic and molecular masses:

where 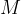 is the kilomolar mass and
is the kilomolar mass and 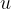 is the atomic mass unit and is given as:
is the atomic mass unit and is given as:
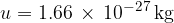
Let's insert equation 3 into equation 2 and obtain:
The specific heat is derived for constant volume since the gas in the container is confined and can not expand. It applies to noble gases where atoms do not combine into larger molecules - e.g. helium, neon, argon, etc. In polyatomic molecules, the internal energy is not only in the kinetic energy of the molecule but also in the movement of the atoms within the molecule. Therefore, their internal energy is greater than calculated.
Very often, however, we observe a change in energy when we change only the temperature. Since it is a change in heat, we denote the formula by 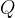 and write:
and write:

Equation (4) applies to all substances, not only to an ideal gas. Heating of substances can be done at constant pressure or at constant volume. Based on this, we add the index 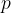 or
or 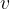 to the specific heat capacity
to the specific heat capacity  - see also, The First Law of Thermodynamics.
- see also, The First Law of Thermodynamics.
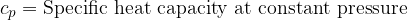

The product of mass 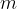 and specific heat capacity
and specific heat capacity  is called heat capacity
is called heat capacity 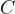 . It tells us how much heat
. It tells us how much heat 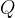 is required to increase the temperature of a substance by
is required to increase the temperature of a substance by 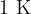 .
.
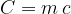
Equation 4 now becomes:
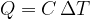
The heat quantity 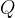 supplied or removed is proportional to the mass
supplied or removed is proportional to the mass 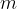 and the change in temperature
and the change in temperature 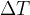 :
:
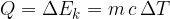
The proportionality factor  is the specific heat capacity:
is the specific heat capacity:
Specific heat capacity tells how much heat we need to increase the temperature of 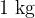 of a substance by
of a substance by 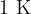 or how much heat we have to remove from the substance to reduce its temperature by
or how much heat we have to remove from the substance to reduce its temperature by 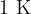 .
.
For monatomic gas molecules, we calculate the specific heat capacity at constant volume using the formula:
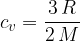
The product of mass 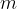 and specific heat capacity
and specific heat capacity  is the heat capacity
is the heat capacity 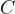 .
.
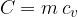
Table of specific heat capacity at constant pressure for some substances:
Let us observe a system in which physical changes are taking place. An observed system can be open, closed, or isolated.
Open system
An open system can exchange heat (internal energy), work, and also mass with its surroundings.
Closed system
A closed system can only exchange heat (internal energy) and work with its surroundings. The mass remains the same.
Isolated system
An isolated system can exchange neither work nor heat with its surroundings.
Let's expand the existing knowledge about the work-energy theorem.
We are observing a closed system, that is, a system that can exchange heat and work with its surroundings, but cannot exchange mass particles.
The extended work-energy theorem states that the sum of the work 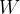 of a force applied to and the heat quantity
of a force applied to and the heat quantity 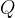 supplied or removed from a system is equal to the change in the total energy of the system:
supplied or removed from a system is equal to the change in the total energy of the system:
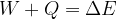
The change in the total energy 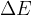 of the system is equal to the sum of the change in the kinetic energy
of the system is equal to the sum of the change in the kinetic energy  , potential energy
, potential energy 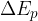 , elastic energy
, elastic energy 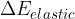 , and internal energy
, and internal energy 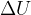 of the system:
of the system:
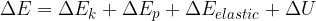
If we add (or remove) work 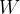 and heat
and heat 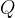 to a physical system, its total energy changes and it's given as:
to a physical system, its total energy changes and it's given as:
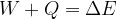
Taking into account the internal energy, the total energy of the system is equal to the sum of kinetic, potential, elastic, and internal energy:
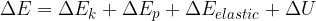
The general form of the energy theorem is therefore given as:
