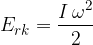Personal collections


Kinetic energy is a type of energy that a body has due to motion. The motion can be straight (linear) or curvilinear. A special form of curvilinear motion is circling or rotation.
In this chapter, we will learn about the kinetic energy of a body in linear motion and circular motion. We will see how the body's energy changes under the influence of external forces  along the distance
along the distance  - i.e. with the force work. Kinetic energy is denoted by the letter
- i.e. with the force work. Kinetic energy is denoted by the letter  , to which, in order to distinguish it from other energies, we add the letter
, to which, in order to distinguish it from other energies, we add the letter  :
:

How does a body acquire kinetic energy?
First, let's assume the body is stationary. At rest according to Newton's first law, it means that no force is acting on the body, or that the sum of all forces acting on it is zero.
What if the sum of all the forces on the body is not zero? According to Newton's second law, a body under the influence of an external force  will begin to move with uniform acceleration
will begin to move with uniform acceleration 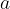 :
:

In time 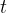 , it will cover a distance
, it will cover a distance  which is given as:
which is given as:

The product of force and distance is the work done by the force:

The unit of work (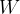 ) is Joule and the symbol is
) is Joule and the symbol is 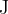 . Since we know that the unit of force (
. Since we know that the unit of force (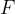 ) is Newton with the symbol
) is Newton with the symbol 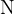 and that of the distance (
and that of the distance ( ) is the metre with the symbol
) is the metre with the symbol 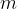 , we can derive the unit Joule from the above formula:
, we can derive the unit Joule from the above formula:
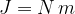
Let's insert the formula of force 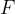 and the distance
and the distance  into equation 1 above:
into equation 1 above:
Therefore, with work, a body of mass 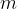 is accelerated to the speed
is accelerated to the speed  . We say the body has been given kinetic energy (kinematos is the Greek word for motion). This is just one of the forms of energy that we give a body through work. We will get to know the others in other chapters.
. We say the body has been given kinetic energy (kinematos is the Greek word for motion). This is just one of the forms of energy that we give a body through work. We will get to know the others in other chapters.
Kinetic energy  is the energy that a body of mass
is the energy that a body of mass 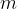 has if it moves with speed
has if it moves with speed  :
:
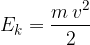
The unit of work and energy and the same which is the Joule (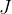 ).
).
With the work of a force, we can change the kinetic energy of a body.
If the work of the force is positive - which means that the force acts in the same direction as the direction of motion of the body - the kinetic energy increases. The body accelerates uniformly. If the work of the force is negative - the force acts in the opposite direction to the motion of the body - the body's kinetic energy decreases and the body decelerates (see Figure 1).
The work-kinetic energy theorem states that the work 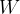 done by a force is equal to the change in kinetic energy - that is, the final kinetic energy
done by a force is equal to the change in kinetic energy - that is, the final kinetic energy 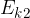 minus the initial kinetic energy
minus the initial kinetic energy 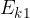 :
:

In summary,
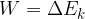
A small body of mass 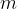 (point body) rotates with tangential or linear speed
(point body) rotates with tangential or linear speed  along a circular path with radius
along a circular path with radius  . We have taken a small body so that we can assume that all points of the body move at the same speed.
. We have taken a small body so that we can assume that all points of the body move at the same speed.
Even in the case of rotation (spinning, circling) of a body, the kinetic energy is considered to be:
We have obtained an expression for the rotational kinetic energy of a body.
The rotational kinetic energy of a body is given as:
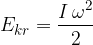
where 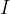 is the moment of inertia of a point body and is given as:
is the moment of inertia of a point body and is given as:

Intuitively, the concept of moment of inertia can be imagined by comparing the equations for translational and rotational kinetic energy which are given as:
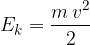
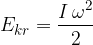
Just as the mass 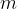 in the first equation represents a property of the body (the greater the mass, the more difficult it is to move the body), so the moment of inertia
in the first equation represents a property of the body (the greater the mass, the more difficult it is to move the body), so the moment of inertia 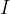 in the second equation represents a property of the body (the greater the moment of inertia, the more difficult it is to prepare the body to rotate).
in the second equation represents a property of the body (the greater the moment of inertia, the more difficult it is to prepare the body to rotate).
Let's look at the concept more closely; let's start with a figure:
The moment of inertia of a composite, real body is obtained by adding up the moments of inertia of the individual elementary masses (or "point" bodies) of which the body is composed.
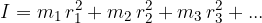
In most cases, the calculation of the moments of inertia of geometric bodies is too complicated to be given here and requires knowledge of integration. Therefore, we will list the moments of inertia for some of the most common bodies in a table.
The table below shows the moments of inertia of some homogeneous bodies rotating about a symmetrical axis:
Let's take a sphere and a cylinder and simultaneously drop them down a slope of height  . The bodies roll down the slope. They do not reach the base of the slope at the same time. The sphere will be faster than the cylinder. Why is that?
. The bodies roll down the slope. They do not reach the base of the slope at the same time. The sphere will be faster than the cylinder. Why is that?
We suspect that the potential energy will be converted into the two types of kinetic energy that we learned about in this material:
the kinetic energy due to the motion of the centre of gravity of the bodies, which is called the translational kinetic energy  and
and
the kinetic energy due to the rotation of the bodies, called rotational kinetic energy 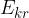 .
.
We express this mathematically as:
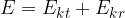
Let’s look at these two kinetic energies more closely.
Let's consider a cylinder or sphere rolling on a horizontal surface and imagine a rolling body as a body that consists of many particles of small masses 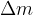 . Let's look at one of these small particles (see Figure 3). The particle moves along a curve path with a speed
. Let's look at one of these small particles (see Figure 3). The particle moves along a curve path with a speed  . The path is drawn in green.
. The path is drawn in green.
We can see that the speed of the particle is not constant but changes. How it changes depends on the position of the observed mass particle - see the velocity vectors in Figure 3 (green).
At any moment, the velocity of any mass particle is equal to the vector sum of two velocities:
the velocity 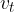 of the centre of gravity, and
of the centre of gravity, and
the tangential velocity 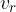 of the particle rotating at a distance
of the particle rotating at a distance  from the centre of gravity:
from the centre of gravity: 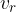
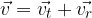
The kinetic energy of the selected particle is therefore:
The kinetic energy of a rolling body consists of two parts: translational kinetic energy and rotational kinetic energy:
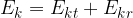
Translational kinetic energy  is the kinetic energy of mass
is the kinetic energy of mass 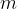 situated in the centre of gravity of a body moving with the speed
situated in the centre of gravity of a body moving with the speed 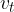 of the centre of gravity:
of the centre of gravity:
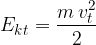
Rotational kinetic energy  is the kinetic energy resulting from the rotation of a body:
is the kinetic energy resulting from the rotation of a body: