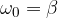Personal collections


Oscillation is a periodic (repeated) movement of a body around a stable equilibrium position. Devices or bodies that oscillate are pendulums. In physics, we know mechanical pendulums and electrical oscillating circuits.
In this material we will focus on mechanical pendulums. Examples of such pendulums are shown in Figure 1.

Figure 1: Examples of mechanical pendulums: helical spring pendulum, gravity pendulum, pendulum with clamped flexible tabs - a musical instrument, Newton's pendulum - a combination of oscillation and collision
Mechanical pendulums are physical devices where potential or elastic energy is periodically converted into kinetic energy of the oscillating body and vice versa. This results in two basic types of pendulums:
Elastic pendulum; an example of an elastic pendulum is:
Gravity pendulum; an example of a gravity pendulum is:
You can as well learn some other mechanical pendulums listed below:
In this material, we will find the answers to the following questions:
How does a body oscillate?
How does the energy of a body change during oscillation?
What are forced oscillation and resonance?
What is damped oscillation?
Let's take an example of oscillation that we know from childhood, the swing:
Let's describe the figure:
The child sits on the swing chair. If no force acts on it, he rests in the lowest position. Let's call it the equilibrium position (position B in Figure 2).
The father pulls the child towards him so that he reaches the extreme position. In the extreme position, the child rises by a height 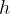 above the equilibrium position. he gains potential energy (position A in Figure 2).
above the equilibrium position. he gains potential energy (position A in Figure 2).
The father releases the child and he begins to swing. In the lower (equilibrium) position, he has the highest speed - the highest kinetic energy, since (almost) all potential energy has been converted into kinetic energy.
We observe the child moving away from the equilibrium position. At some point, he is away from the equilibrium position by a distance 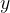 (position C in Figure 2). This distance is called displacement from the equilibrium position.
(position C in Figure 2). This distance is called displacement from the equilibrium position.
The speed (kinetic energy) of the child decreases and his potential energy increases until it reaches the opposite extreme position (position D in Figure 2). The distance he covers is called the maximum displacement from the equilibrium position or amplitude. Let's denote it by 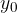 .
.
From this moment, he moves in the same way in the opposite direction until he reaches its original position.
The entire path he travelled from and back to his original (initial) position is called one oscillation. The time it takes to make one oscillation is called the period  . The reciprocal of the period is the natural frequency
. The reciprocal of the period is the natural frequency 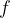 of the oscillation:
of the oscillation:

The oscillation is repeated.
If the child just sits passively in the chair and does not push himself away with his legs, the oscillation gradually dies down. The reason for this is friction in the axes of the swing and air resistance. The amplitude of the oscillation decreases and finally drops to zero. Such oscillation is called damped oscillation.
To ensure that the swing does not die out too soon, the father can help him by pushing him repeatedly when he swings to his side. He adds kinetic energy to it, which replaces the energy lost due to friction. Such oscillation is called forced oscillation. If the father adds energy at equal time intervals equal to the period of oscillation of the child, then with the least added energy he achieves the maximum amplitude of the oscillation of the child. In this case, the child oscillates with a resonant frequency.
If the instantaneous value of the displacement of the body from its equilibrium position is a sinusoidal function of time, the oscillation will be harmonic. In this case, all the formulas and equations derived in the material, Simple harmonic motion apply.
Real pendulums rarely oscillate perfectly harmoniously. The closest thing to harmonic oscillation is a spring pendulum, where Hooke's law applies. A pendulum generally does not oscillate harmonically. It oscillates approximately harmonically only at sufficiently small amplitudes, which can be seen in the material, Simple pendulum.
In the material, Simple harmonic motion, we learned about some basic concepts and equations that apply to harmonic or sinusoidal oscillation. We also learned how to make a pendulum that oscillates harmonically and how to calculate its period and frequency in the materials, Helical spring pendulum and Simple pendulum.
In the section, Description of oscillation, we learned that oscillation is basically a periodic (repeated) conversion of energy from one form to another.
To oscillate a pendulum, we must move the body from the equilibrium position for the maximum displacement 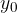 . In doing so, we do work and give it potential or elastic energy. When the body is released, the original energy decreases, and the kinetic energy increases. Its speed increases and reaches its maximum value in the equilibrium position when all the energy is converted into kinetic energy. The process is repeated in the reverse direction: the speed and thus the kinetic energy of the body decreases and is finally converted into the same energy as it was at the beginning.
. In doing so, we do work and give it potential or elastic energy. When the body is released, the original energy decreases, and the kinetic energy increases. Its speed increases and reaches its maximum value in the equilibrium position when all the energy is converted into kinetic energy. The process is repeated in the reverse direction: the speed and thus the kinetic energy of the body decreases and is finally converted into the same energy as it was at the beginning.
It is assumed that in the case of undamped oscillation of a spring pendulum, the sum of elastic energy 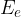 and kinetic energy
and kinetic energy  is constant at all displacements from the equilibrium position. It is equal to the maximum kinetic energy
is constant at all displacements from the equilibrium position. It is equal to the maximum kinetic energy  or maximum elastic energy
or maximum elastic energy 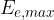 :
:
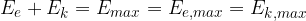
In the undamped oscillation of a simple pendulum, the sum of potential energy 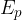 and kinetic energy
and kinetic energy  is constant at all displacements from the equilibrium position and is equal to the maximum kinetic energy
is constant at all displacements from the equilibrium position and is equal to the maximum kinetic energy  or maximum potential energy
or maximum potential energy 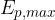 :
:
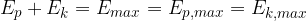
Let us demonstrate this statement on a spring pendulum.
The spring pendulum is described in more detail in the material, Helical spring pendulum. For our current needs, let's take a spring pendulum in a horizontal position. A mass 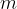 is attached to a spring with a spring constant
is attached to a spring with a spring constant  , which can oscillate without friction on a horizontal surface (see the figure in the material, Helical spring pendulum).
, which can oscillate without friction on a horizontal surface (see the figure in the material, Helical spring pendulum).
Let's assume that the oscillation is not damped. The amplitude is constant.
The energy of oscillation at any moment is equal to the sum of elastic and kinetic energy:
The sum of the elastic and kinetic energy of a pendulum on a helical spring is equal to the maximum energy of the pendulum at any moment.

or:
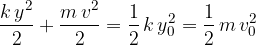
Let's imagine a pendulum in the form of a steel tab clamped on one side (see Stationary transverse wave ). The tab is moved away from the equilibrium position and released so that it oscillates with its own frequency 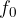 . The oscillation is damped, its amplitude gradually drops to zero.
. The oscillation is damped, its amplitude gradually drops to zero.
Let's now place an electromagnet under the steel tab and connect an AC voltage generator to it. With the help of an alternating magnetic field, the electromagnet exerts a force on the tab so that it oscillates with the frequency imposed on it by the generator - Figure 4.
If we change the frequency of the generator, we also change the frequency of the forced oscillation - and thus also the amplitude of the oscillation. We are interested in how the amplitude of the oscillation changes depending on the frequency.
We find this out by measuring the amplitude of the tad oscillation at different frequencies and plotting a graph (see Figure 5). We get the resonance curve of the pendulum. We notice that the pendulum oscillates most strongly when the imposed frequency is equal to the natural frequency of the pendulum. We say that then the generator and the pendulum are in resonance.
How much amplitude the pendulum reaches in resonance depends on the damping. At higher damping, the amplitude is lower (dashed line in Figure 5), and at lower damping, it is higher (solid line).
Due to friction or air resistance, the amplitude of the oscillation decreases until it drops to zero. Friction and air resistance do negative work, and the energy of the oscillation decreases. The oscillation is damped.
Let's assume that the cause of damping is air resistance. In this case, the oscillation amplitude decreases according to the following equation:
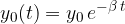
where:
 is the natural number 2.71,
is the natural number 2.71,
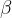 is the damping coefficient,
is the damping coefficient,
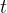 is time,
is time,
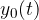 is the amplitude of the oscillation at time
is the amplitude of the oscillation at time 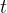 ,
,
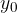 is the initial amplitude of the oscillation.
is the initial amplitude of the oscillation.
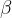 is equal to the reciprocal of the time when the oscillation amplitude decreases by
is equal to the reciprocal of the time when the oscillation amplitude decreases by  -times. Let's calculate the factor by which the amplitude then drops (see also Figure 6):
-times. Let's calculate the factor by which the amplitude then drops (see also Figure 6):
Due to damping, the natural frequency of the pendulum is also reduced. The derivation of the calculation of the natural frequency of a damped oscillation is more demanding, so we only give the result here:
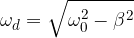
From the equation, we can understand an interesting fact that the natural frequency can drop to zero. This happens when:
This is a limiting case when the pendulum, after being released, no longer passes through the equilibrium position but stops in the equilibrium position. We say that the pendulum is critically damped (dashed red curve in Figure 6).
In the case of damped oscillation, the oscillation amplitude decreases according to the formula:
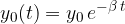
In doing so, there is a damping factor 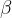 . It is equal to the reciprocal of the time during which the oscillation amplitude decreases by
. It is equal to the reciprocal of the time during which the oscillation amplitude decreases by  - times.
- times.
Damping also reduces the natural frequency of oscillation. It can be calculated using the formula:
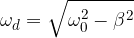
A pendulum is critically damped when it swings from one extreme position only to the equilibrium position (and does not swing around the equilibrium position) and then stops. The condition for critical damping is: