Personal collections


When we calculated the work of a force, we did not take into account how much time the work was done, e.g. in what time did we accelerate a car to a certain speed 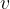 and give it kinetic energy or lift a load to a height
and give it kinetic energy or lift a load to a height 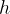 and give it potential energy or tension a spring with a force constant
and give it potential energy or tension a spring with a force constant 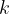 and give it elastic energy.
and give it elastic energy.
Now we will also consider time. For this purpose, we introduce the physical quantity called power. The greater the power e.g. of a machine, the greater the amount of work it does in a given time.
Power is therefore defined as the work done per unit time:
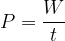
The power is denoted by 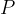 and its SI unit is Watt (
and its SI unit is Watt (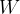 ). From the equation, the unit of power is:
). From the equation, the unit of power is:
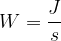
which we read as "Joule per second".
From the equation for power, let's make work the subject:
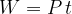
the unit of work, expressed in terms of the unit of power (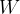 ), is:
), is:
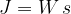
Using the knowledge from the chapter, work of a force, the equation for the work of a force can be written in two forms:
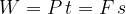
and consequently, the unit of work is:
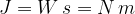
Power is work per unit time:
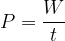
the unit of power is:
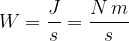
which we read as: Watt, Joule per second, and Newton metre per second.
The work is:
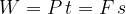
and its unit is:
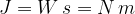
which we read as: Joule, Watt second, Newton metre.
If a constant force 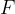 acts on a body during a linear motion, it moves with uniform acceleration. The Force therefore performs work and with the distance
acts on a body during a linear motion, it moves with uniform acceleration. The Force therefore performs work and with the distance  travelled, the body's velocity
travelled, the body's velocity 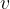 increases (or decreases - depending on the direction of the force), and thus its kinetic energy.
increases (or decreases - depending on the direction of the force), and thus its kinetic energy.
When a body moves a distance 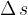 in a short time interval
in a short time interval 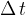 , the work done is given as:
, the work done is given as:
In a straight-line motion, the power at constant force 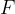 depends on the distance
depends on the distance  and time
and time 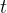 .
.
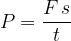
At the moment of observation, when the body reaches velocity 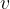 , the power is:
, the power is:
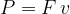
In rotation, we assume that a constant torque  acts on the body. The angular velocity
acts on the body. The angular velocity 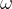 of the body increases uniformly - see the theory, Torque, if the torque acts in the direction of rotation, decreases uniformly if it acts in the opposite direction, or remains constant if the torque is zero.
of the body increases uniformly - see the theory, Torque, if the torque acts in the direction of rotation, decreases uniformly if it acts in the opposite direction, or remains constant if the torque is zero.
When the body rotates through an angular displacement 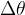 in a short time interval
in a short time interval 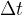 , the work done is given as:
, the work done is given as:
Power in rotational motion is the product of torque  and angular velocity
and angular velocity 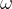 :
:
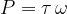
A pulley (or gear) transfers the rotational power from the first roller to the second roller. In doing so, the angular speed (or frequency) of rotation of the second roller and the torque can be changed.
The belt connects two parallel rollers, with radii 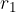 and
and 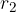 as shown in the figure below:
as shown in the figure below:
Let an electric motor with power 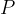 be connected to the first roller. The power is transmitted via a pulley to the second roller. The first roller rotates with angular velocity
be connected to the first roller. The power is transmitted via a pulley to the second roller. The first roller rotates with angular velocity  , and the second with
, and the second with 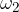 . Therefore:
. Therefore:
the force 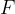 along the belt is the same everywhere as it is the internal force of the belt.
along the belt is the same everywhere as it is the internal force of the belt.
If the statement were not true, there would have to be a point on the belt - let it be point T - where the force just before point T would be different from the force at point T. Since there would be two different forces acting on the same sections of the belt, we would see a section of the belt a little before point T, moves faster (or slower) than the section at point T. But when the belt rotates, we do not notice this, so the force along the belt must always be the same.
The angular velocities of both rollers are inversely proportional to the radius.
Let's prove this statement by first realizing that the speed 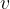 of the belt is equal to the tangential speed of the two rollers (if the belt does not slip). It follows from this that:
of the belt is equal to the tangential speed of the two rollers (if the belt does not slip). It follows from this that:
The power is the same on both rollers.
This statement can be shown using the formula of power which is given as:
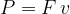
The force 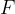 is the same on both rollers, as is the tangential speed
is the same on both rollers, as is the tangential speed 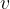 . It follows that the powers are the same.
. It follows that the powers are the same.
The torque on both rollers is proportional to the radius of the rollers and inversely proportional to the angular velocities (or frequencies) of both rollers.
Let's prove the statement by first writing out the torque equations that apply to both rollers:
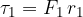
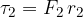
We divide the equation and and note that  :
:
In the chapter, elastic energy, the energy equation was given as:
The sum of all energies is the total energy 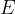 of the body. In total energy, for now, we only consider kinetic, potential, and elastic energy:
of the body. In total energy, for now, we only consider kinetic, potential, and elastic energy:
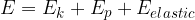
and write simply:
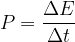
Power tells how fast the total energy of a body changes and is given as:
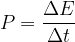
where 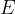 is the sum of kinetic, potential, and elastic energy.
is the sum of kinetic, potential, and elastic energy.