We have already come across viscosity in the chapter, Bernoulli's Equation. Here, we will get to know it in a little more detail.
Viscosity is a property of liquids that causes:
obstruction to the movement of the liquid itself, or
the retarding force on a body moving in a (viscous) fluid.
We have already learned about the braking force on a body moving in a liquid in the material, Bernoulli's Equation, where we named the law, the square law of resistance.
But let's go back to viscosity: how does it manifest itself in nature? Let's look at some examples.
Examples show the influence of different viscosities on the physical properties of liquids. Because of its lower viscosity, water flows faster than oil or honey. Due to its high viscosity, it is difficult to mix honey. The viscosity of honey decreases when it is heated. The same applies to other liquids. Heated oil is less viscous than cold. Due to viscosity, the river flow is faster in the middle of the channel than near the bank and faster on the surface than at the bottom.
Viscosity occurs as internal friction between layers of moving fluid. It does not matter whether the fluid is moving relative to a stationary bed (or pipe) or whether an object is moving in a stationary fluid. In the case of water flowing through a pipe, the velocity of the water right next to the pipe is zero, and it is greatest in the centre of the pipe. The same applies to a moving boat on still water: the layer of water right next to the boat moves at the same speed as the boat, if we move away from the boat, the speed of the water drops to zero.
The mechanism of internal friction is not the same as the mechanism we learned about in the chapter, Friction and Bonding Force. In liquids, there is no frictional force that we have to overcome in order for the body to start moving. The braking force caused by viscosity is proportional to speed. If the speed is zero, the braking force is also zero.
Let's define viscosity:
Viscosity is a measure of a fluid's resistance to the shear stresses acting on the fluid layer during motion.
The statement needs a little more explanation, so let's look at the experiment shown in Figure 2. It will lead us to the equation we use to determine viscosity.
Figure 2: Shear force of viscous liquids
We take a liquid of small depth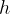 
, on which we place a flat plate of surface 
so that it just touches the surface (see Figure 2). The plate is dragged along the surface by a force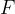 
so that it moves with a small speed 
.
It turns out that the liquid layer directly below the plate also moves at the same speed . It looks like it is glued to the plate - or to put it another way: the plate wants to "shear off" the early liquid layer from the rest of the liquid. Hence the term shear force.
Shear forces also act between all other layers. The nature of these forces is as follows:
In the case of liquids, these are attractive intermolecular forces. These forces decrease with temperature.
In the case of a gas, there are no attractive intermolecular forces. In this case, the motion of gas molecules due to temperature is transferred from one layer to another through collisions (diffusion). Since the shear forces between the layers are due to thermal motion, we expect the forces to be larger at higher temperatures and to drop to zero at temperatures near absolute zero.
The listed forces are quite weak, so the transfer of motion to the next layer is not complete. The next layer will never reach the speed of the previous layer. The motion is thus transferred from layer to layer in such a way that the speed decreases slightly with each successive layer. At the bottom, the last layer "sticks" to the stationary base and is therefore also stationary (see the plotted velocity curves in Figure 2).
With water, oil, and air, we notice that the velocity actually decreases linearly from the moving plate to the stationary bottom. The condition is that the depth 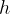and the velocity are small. Fluids that behave according to this finding are called Newtonian fluids (after the physicist, Isaac Newton). This law, however, is not characteristic of all liquids; the graph of the relationship between the velocity and depth 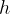can be non-linear.
Newton gave the equation for the relationship between the ratio 
and the ratio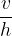 
and it applies to Newtonian fluids:
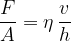
Where:
the factor is called the tangential or shear stress. The expression is the same as for pressure, except that instead of perpendicular (as in pressure), the force acts in the direction of the surface. The unit is the same as for pressure, so:
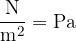
the factor 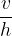is called the velocity gradient or shear rate.
the proportionality constant 
is called coefficient of viscosity of the liquid.
Let's make the subject of the above equation:
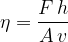
and its unit is:
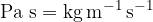
The table below shows the viscosities and densities of some substances at a temperature of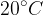 
and pressure of 
:
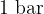Viscosity is the proportionality coefficient between the tangential or shear stress and the velocity gradient or shear rate :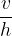
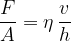
The unit for viscosity is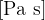 
(Pascal second).
A small object is completely immersed in a stationary, viscous liquid and moves slowly in it (the liquid can also be moving and the object is stationary). The requirement that the object be small and the speed be small is given so that the moving object does not cause the fluid to swirl, which would increase drag.
As we learned in the previous chapter, the layer of liquid right next to a moving object will move at the same speed as the object (see the velocity vectors - red arrows - in Figure 3). The layer of liquid right next to the body will act with a shear or tangential force on the adjacent layer so that it will start to move at a slightly lower speed. The speed of each adjacent layer is slightly lower - therefore, the layers of the liquid that are far enough away from the object are at rest (they are not affected by the movement of the object).
Figure 3: Drag force of a viscous fluid on a ball
In the above section, we found that for a plate with a surface , moving at a speed along the surface of a viscous liquid with a depth or thickness 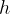, Newton's equation is given as:
We got the force we need to pull on the plate to keep the speed of motion in the fluid constant. Its opposite force is the drag or resistance force of the liquid which is therefore given as:
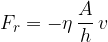
The drag force is directly proportional to the speed, so this is the linear drag law.
In the event that the linear drag law applies, we can write down the resistance or drag force of the fluid on the body with the general equation:
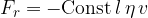
where 
is the length of the frontal section of the body.
Indeed, the derivation of the linear resistance force for a concrete body is quite challenging. At this point, without derivation, we write that for a ball with radius 
:
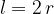
The drag force on a ball moving in a viscous fluid is therefore:
For a small body moving with a small speed in a viscous fluid with viscosity , the linear law of resistance applies:
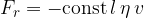
where is the length of the frontal section of the body (for a sphere, this length is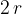 
).
For a small ball, the linear law of resistance (Stoke's law) is given as:
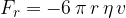
We are often in a dilemma whether we should use the linear or quadratic law of resistance when calculating the resistance force. The decision to use one or another law is based on the calculation of the Reynolds number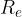 
. We calculate it according to the equation:
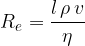
where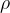 
is the density of the liquid. In the case of a sphere, we take 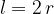, we therefore have:
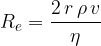
The Reynolds number is applied according to the following rules:
If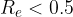 
, we use the linear law of resistance.
If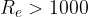 
, we use the quadratic law of resistance.
If 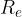is in the intermediate region, neither of these two laws apply.
The Reynolds number for a sphere of radius moving at a speed in a liquid of viscosity and density 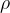is calculated using the formula:
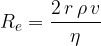
With the help of the Reynolds number, we check whether the linear or quadratic law of drag applies. If 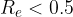, we use the linear law of resistance, if 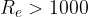, we use the quadratic law of resistance, for intermediate results neither of these two laws applies.
