Personal collections


In the chapter, Thermal Equilibrium, we discussed the case when all bodies in a thermal-insulated container (called a calorimeter) reach the same temperature after a certain time. This state is the equilibrium state. The equilibrium state can only be approximately reached in the laboratory by inserting it into the equation for thermal theoretical conditions for measuring purposes - e.g. for measuring the specific heat capacities of certain substances. There is no such state in nature. Some call it "thermal death" because in such a state there would be no wind, no weather phenomena, and no heat engines would work, and in short, life on planet Earth would not be possible.
The concept of heat transfer includes various mechanisms of heat transfer from body to body and heat spread within the body. For the sake of systematics, we will use the example below to name the different mechanisms, and in the following, we will focus on the conduction and radiation of heat, which are the easiest to understand computationally.
Although we will get to know the mechanisms of heat transfer on a concrete example, the phenomena are general.
The mechanisms of heat transfer are most easily understood in the example of heating an apartment. Let's sketch an example:
Figure 1 shows the following quantities:
radiator temperature 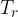
inside temperature 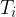
inner wall temperature 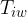
outside temperature 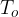
outer wall temperature 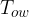
A heated radiator emits heat into the room in three ways:
Heat transfer
We speak of heat transfer when heat passes from one substance to another, e.g. from water to metal, from metal to air, etc. The mechanism of heat transfer is theoretically very demanding. Let's just mention that the greater the temperature difference between the radiator and the room and the faster the air circulates around the radiator, the greater the heat transfer. The circulation can be due to natural convection or the circulation can be forced, e.g. with the help of a fan.
Air convection
Heated air rises near the radiator due to upthrust as it has a lower density than cold air. It cools on the ceiling and falls back to the ground. The process is repeated.
Heat radiation
The radiator also radiates heat - it emits infrared rays. These are rays that travel at the speed of light and have a wavelength longer than that of visible light - greater than 750 nm in vacuum or air. The higher the temperature of the radiator and the lower the ambient temperature, the higher its radiation.
The heat from the apartment is transferred to the external wall and from the external wall to the external air. Due to heat transfer, the inner part of the outer wall is always at a slightly lower temperature than the room temperature and the outer part of the outer wall is at a slightly higher temperature than the surrounding air temperature - see Figure 1. Similar to the radiator, this heat transfer also depends on air velocities at the walls, e.g. because of the wind.
The wall itself conducts heat. Due to thermal contact between molecules, kinetic energy is transferred from faster molecules to slower molecules through collisions. We are talking about heat flow. This flows from a higher temperature to a lower temperature.
If the radiator emits the same amount of heat during the observed time as is lost due to heat flow, the apartment is always at the same temperature. We are talking about a steady state.
Heat spreads in different ways:
Heat transfer is when heat passes from one substance to another (metal - air, water - metal, etc...)
Heat convection is the circulation of heat due to upthrust: a warm substance (air, water) rises, cold one falls.
Heat conduction is the propagation of heat within a substance due to collisions of molecules that move due to heat.
Radiant heat is an electromagnetic wave similar to radio waves or visible light. So it spreads at the speed of light.
As we mentioned in the example above, heat spreads through matter from a higher temperature to a lower temperature. We say that matter conducts heat. A substance can conduct heat well or poorly, so substances can be roughly divided into:
heat conductors
heat insulators
The substance through which heat is propagated can be:
homogeneous; this means it conducts heat equally everywhere and the temperature within the substance drops uniformly from a place with a higher temperature to a place with a lower temperature.
inhomogeneous; this means that it conducts heat differently in different parts (e.g. a substance that consists of several layers with different thermal conductivity.)
The heat flow rate or heat flux by conduction tells us how many joules per second of heat pass through a substance.

The heat flux is denoted by 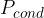 and its unit is the same as the unit of power which is
and its unit is the same as the unit of power which is 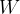 (watts).
(watts).
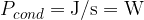
The formula of heat flow rate through a certain substance can be derived. The greater the cross-sectional area  of the substance through which the heat flows (e.g. wall surface), the smaller the distance
of the substance through which the heat flows (e.g. wall surface), the smaller the distance 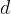 that the heat flow must travel (e.g. wall thickness) and the greater the temperature difference
that the heat flow must travel (e.g. wall thickness) and the greater the temperature difference 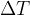 at both ends of the substance, the greater the heat flow rate
at both ends of the substance, the greater the heat flow rate 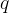 .
.
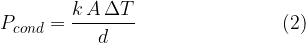
The proportionality constant 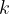 is called the thermal conductivity coefficient of the substance.
is called the thermal conductivity coefficient of the substance.
Expressing the coefficient of thermal conductivity 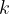 as the subject of the formula, we have:
as the subject of the formula, we have:
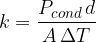
From the equation, we can deduce the unit of the thermal conductivity which is given as:
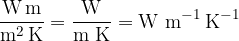
The fraction 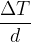 in equation (2) is also called the temperature gradient. It tells us how fast the temperature changes with the distance
in equation (2) is also called the temperature gradient. It tells us how fast the temperature changes with the distance  in the direction of heat flow. Since the temperature in the direction of heat flow decreases, we have:
in the direction of heat flow. Since the temperature in the direction of heat flow decreases, we have:

Heat flux tells us how much heat passes through a substance per time:
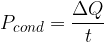
The unit is joules per second ( ) or watts (
) or watts (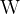 ).
).
The heat flux is calculated using the formula:
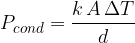
where  is the coefficient of thermal conductivity,
is the coefficient of thermal conductivity,  is the cross-sectional area of the substance through which heat flows, and
is the cross-sectional area of the substance through which heat flows, and 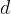 is the length of heat flow.
is the length of heat flow.
The term 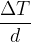 is called the temperature gradient. It tells us how the temperature changes in the direction of the heat flow.
is called the temperature gradient. It tells us how the temperature changes in the direction of the heat flow.
Let's look at the thermal conductivity  for some typical substances:
for some typical substances:
The formula for heat flow is similar to what the formula for conductivity and current through conductors is in electricity (see the chapter, Electrical resistance). We will see this more clearly if we re-adjust equation 2 as follows:
Suppose heat passes through several substances with different thicknesses and different thermal conductivity. In that case, the thermal resistances are added up in a similar way as the electrical resistances are added up when resistors are connected in series:
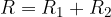
The heat flux can be written using the expression:
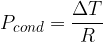
where 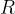 is thermal resistance. When several substances are bonded in series, the thermal resistances are added together.
is thermal resistance. When several substances are bonded in series, the thermal resistances are added together.
Any body heated to a certain temperature 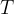 has a heat flow rate or heat flux by radiation
has a heat flow rate or heat flux by radiation  that is proportional to the surface area
that is proportional to the surface area  of the body and the fourth power of the absolute temperature
of the body and the fourth power of the absolute temperature 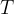 (that is, the temperature in Kelvin):
(that is, the temperature in Kelvin):

The proportionality factor that connects the quantities is Stefan's constant 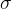 which is given as:
which is given as:
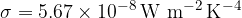
If we divide equation 4 by  , we get the radiant flux density
, we get the radiant flux density  :
:
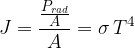
The equation is called Stefan's law and applies to black-body radiation. If the body is not black, we must consider the emissivity factor  (radiation capacity) of the body, and the formula therefore becomes:
(radiation capacity) of the body, and the formula therefore becomes:
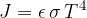
For a black body,  is equal to 1, for light and dry soils 0.9, and for dark and wet soils 0.98. Water emissivity is between 0.92 and 0.97. The emissivity of the smooth silver surface is 0.
is equal to 1, for light and dry soils 0.9, and for dark and wet soils 0.98. Water emissivity is between 0.92 and 0.97. The emissivity of the smooth silver surface is 0.
A black body radiates heat according to Stefan's law. The radiant flux is given as:
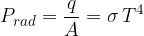
Stefan's constant is given as: